题目内容
17.已知等差数列{an}的首项为$\frac{1}{2}$,Sn为数列的前n项和,若S6=2S4,则a10=( )| A. | $\frac{1}{3}$ | B. | $\frac{19}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
分析 设等差数列{an}的公差为d,由题意和等差数列的前n项和公式列出方程,求出公差d的值,代入等差数列的通项公式求出a10的值.
解答 解:设等差数列{an}的公差为d,
∵等差数列{an}的首项为$\frac{1}{2}$,S6=2S4,
∴$6×\frac{1}{2}+\frac{6×5}{2}×d=2(4×\frac{1}{2}+\frac{4×3}{2}×d)$,
解得d=$\frac{1}{3}$,
∴a10=$\frac{1}{2}+9×\frac{1}{3}$=$\frac{7}{2}$,
故选:D.
点评 本题考查了等差数列的通项公式,以及等差数列的前n项和公式应用,属于基础题.

练习册系列答案
相关题目
8.$\sqrt{1-2sin(\frac{π}{2}+2)cos(\frac{π}{2}+2)}$的值是( )
| A. | sin2-cos2 | B. | cos2-sin2 | C. | -(sin2+cos2) | D. | sin2+cos2 |
5.已知x,y满足约束条件$\left\{\begin{array}{l}2x+y-2≥0\\ x-2y+4≥0\\ 3x-y-3≤0\end{array}\right.$,目标函数z=x2+y2的最小值为( )
| A. | 13 | B. | $\sqrt{13}$ | C. | $\frac{4}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
12.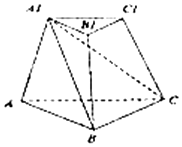 如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )
如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )
 如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )
如图,在三棱台ABC-A1B1C1中,截去三棱锥A1-ABC,则剩余部分是( )| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 五棱锥 |
2.若16x=9y=4,则xy等于( )
| A. | log43 | B. | log49 | C. | log92 | D. | log94 |
9.已知a=2${\;}^{\frac{1}{3}}$,b=log3$\frac{2}{3}$,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,则( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
7.过点(2,1)作圆(x-1)2+(y+2)2=25的弦,其中最短的弦所在的直线方程为( )
| A. | 3x-y-5=0 | B. | x+3y-1=0 | C. | 2x-y-3=0 | D. | x+3y-5=0 |
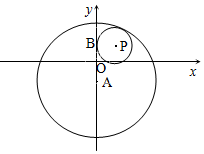 已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.
已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.