题目内容
16.若实数x∈Z,y∈Z,满足$\left\{\begin{array}{l}{x<2}\\{y≤3}\\{x+y≥1}\end{array}\right.$,则S=2x+y-1的最大值为6.分析 由已知得到平面区域,利用目标函数的几何意义求最优解.
解答 解:由题意,xy,满足的区域如图:由 S=2x+y-1的几何意义得到当直线经过图中整点B(2,3)时使得S最大,所以S=2x+y-1的最大值为2×2+3-1=6.
S=2x+y-1的几何意义得到当直线经过图中整点B(2,3)时使得S最大,所以S=2x+y-1的最大值为2×2+3-1=6.
故答案为:6.
点评 本题考查画不等式组表示的平面区域及利用线性规划求函数的最值,关键是给目标函数赋与几何意义

练习册系列答案
相关题目
4.设全集U是实数集R,集合M={x|x2>2x},N=$\left\{{x|\frac{2-x}{x-1}≥0}\right\}$,则(∁UM)∩N为( )
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1<x≤2} | D. | {x|1≤x<2} |
11.下列各组函数中,表示同一函数的是( )
| A. | y=1,y=$\frac{x}{x}$ | B. | y=$\frac{{x}^{2}-x}{x}$与y=x-1 | C. | y=x,y=$\root{3}{{x}^{3}}$ | D. | y=|x|,y=($\sqrt{x}$)2 |
8.$\sqrt{1-2sin(\frac{π}{2}+2)cos(\frac{π}{2}+2)}$的值是( )
| A. | sin2-cos2 | B. | cos2-sin2 | C. | -(sin2+cos2) | D. | sin2+cos2 |
5.已知x,y满足约束条件$\left\{\begin{array}{l}2x+y-2≥0\\ x-2y+4≥0\\ 3x-y-3≤0\end{array}\right.$,目标函数z=x2+y2的最小值为( )
| A. | 13 | B. | $\sqrt{13}$ | C. | $\frac{4}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
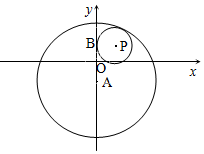 已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.
已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.