题目内容
已知多面体ABCDEF中，AB∥CD∥EF，平面ABCD与平面ADE垂直，△ADE是以AD为斜边的等腰直角三角形，点G为边BC的中点，且AB=AD=2，CD=4，EF=3．（1）求证：FG⊥平面ABCD；
（2）若∠ADC=120°，求二面角F-BD-E的正弦值．
考点：与二面角有关的立体几何综合题,直线与平面垂直的判定
专题：综合题,空间位置关系与距离,空间角
分析：（1）取AD中点O，连接OG、OE，利用面ADE⊥面ABCD，证明EO⊥面ABCD，可证四边形OGFE为平行四边形，从而可得结论；
（2）建立空间坐标系，确定面BDE的法向量、面BDF的法向量，利用向量的夹角公式，可得结论．
（2）建立空间坐标系，确定面BDE的法向量、面BDF的法向量，利用向量的夹角公式，可得结论．
解答：
（1）证明：取AD中点O，连接OG、OE，
∵△ADE为等腰三角形，
∴OE⊥AD…（1分）
∵平面ABCD⊥平面ADE，平面ABCD∩平面ADE=AD，且OE?平面AED，
∴OE⊥平面ABCD…..（3分）
∵AB∥EF∥CD，且O、G分别是AD、BC的中点
∴OG∥EF，OG=3=EF，
∴四边形OGFE是平行四边形，
∴OE∥FG…..（4分）
∴FG⊥平面ABCD．…..（5分）
（2）解：连接OB，
在△ABD中，AD=AB=2，∠DAB=60°，∴△ADB是等边三角形，即OB⊥AD．
由（1）知，OE⊥平面ABCD，分别以
、
、
为x，y，z轴建立如图所示的空间直角坐标系，则
A（1，0，0），B(0，
，0)，D（-1，0，0），E（0，0，1），
利用
=2
及
=
得C(-3，2
，0)、F(-
，
，1)，…．（6分）
设平面BDF的法向量
=(x，y，z)，则
•
=-
x+
y+z=0，
•
=-x-
y=0，
令y=1，则x=-
，z=-2
，
即
=(-
，1，-2
)，|
|=4…（8分）
同理可求平面BDE的法向量为
=(-
，1，
)…（10分）
∴cos＜
，
＞=
=-
…（11分）
∴二面角F-BD-E的正弦值为
．…（12分）
（1）证明：取AD中点O，连接OG、OE，∵△ADE为等腰三角形，
∴OE⊥AD…（1分）
∵平面ABCD⊥平面ADE，平面ABCD∩平面ADE=AD，且OE?平面AED，
∴OE⊥平面ABCD…..（3分）
∵AB∥EF∥CD，且O、G分别是AD、BC的中点
∴OG∥EF，OG=3=EF，
∴四边形OGFE是平行四边形，
∴OE∥FG…..（4分）
∴FG⊥平面ABCD．…..（5分）
（2）解：连接OB，
在△ABD中，AD=AB=2，∠DAB=60°，∴△ADB是等边三角形，即OB⊥AD．
由（1）知，OE⊥平面ABCD，分别以
| OA |
| OB |
| OE |
A（1，0，0），B(0，
| 3 |
利用
| DC |
| AB |
| EF |
| 3 |
| 2 |
| AB |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
设平面BDF的法向量
| n |
| n |
| BF |
| 3 |
| 2 |
| ||
| 2 |
| n |
| BD |
| 3 |
令y=1，则x=-
| 3 |
| 3 |
即
| n |
| 3 |
| 3 |
| n |
同理可求平面BDE的法向量为
| m |
| 3 |
| 3 |
∴cos＜
| n |
| m |
| ||||
|
|
| ||
| 14 |
∴二面角F-BD-E的正弦值为
| ||
| 14 |
点评：本题考查线面垂直，考查面面角，考查利用空间向量解决空间角问题，确定平面的法向量是关键．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）在定义域R内可导，若对x∈R，恒有f（1+x）=f（1-x），且当x∈（-∞，1）时，（x-1）f′（x）＜0，设a=f（0），b=f（
），c=f（3），则（ ）
| 1 |
| 2 |
| A、b＜c＜a |
| B、c＜a＜b |
| C、c＜b＜a |
| D、a＜b＜c |
在长方体ABCD-A1B1C1D1中，∠AB1B=45°，∠CB1C1=60°，则异面直线AB1与A1D所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
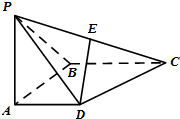如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，且∠PAB=∠ABC=90°，AD∥BC，PA=AB=BC=2AD，E是PC的中点．
如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=2，点E是SD的中点．
如图，在平面直角坐标系xOy中，点A（x1，y1）在单位圆O上，∠xOA=α，且α∈（