题目内容
已知a，b，c∈R，（a+b+c）2≥2（a2+b2+c2）+4d，求证：ab+bc+ac≥3d．
考点：不等式的证明
专题：证明题,函数的性质及应用,不等式的解法及应用
分析：将已知不等式展开，得到c2-2（a+b）c+a2+b2-2ab+4d≤0，运用主元思想，可令f（c）=c2-2（a+b）c+a2+b2-2ab+4d，则f（c）≤0，由判别式不小于0，得到ab≥d，同理，可视a，b为主元，则可证得bc≥d，ac≥d，相加即可得证．
解答：
证明：（a+b+c）2≥2（a2+b2+c2）+4d，展开可得，
c2-2（a+b）c+a2+b2-2ab+4d≤0，
可令f（c）=c2-2（a+b）c+a2+b2-2ab+4d，则f（c）≤0，
由于f（c）的图象表示开口向上的抛物线，且与x轴有交点，
则判别式△=4（a+b）2-4（a2+b2-2ab+4d）≥0，
化简可得，ab≥d，
同理，可视a，b为主元，则可证得bc≥d，ac≥d，
则ab+bc+ac≥3d．
c2-2（a+b）c+a2+b2-2ab+4d≤0，
可令f（c）=c2-2（a+b）c+a2+b2-2ab+4d，则f（c）≤0，
由于f（c）的图象表示开口向上的抛物线，且与x轴有交点，
则判别式△=4（a+b）2-4（a2+b2-2ab+4d）≥0，
化简可得，ab≥d，
同理，可视a，b为主元，则可证得bc≥d，ac≥d，
则ab+bc+ac≥3d．
点评：本题考查不等式的证明，考查运用主元法思想，借助二次函数的图象和性质，考查推理能力，属于中档题．
练习册系列答案
相关题目
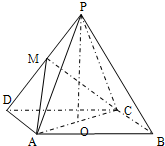如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC，O为AC中点，PO⊥平面ABCD，M为PD中点．若AC=2PO，求二面角P-AB-C的正切值．