题目内容
16.抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为4或6“;事件B为“两颗骰子的点数之和大干8”求事件A发生时,事件B发生的概率是$\frac{5}{12}$.分析 先求出所有可能的事件的总数,及事件A,事件B,事件AB包含的基本事件个数,代入条件概率计算公式,可得答案
解答 解:设事件A为“蓝色骰子的点数为4或6“的概率为P(A)=$\frac{1}{3}$,
两颗骰子的点数之和大干8的6+3,6+4,6+5,6+6,3+6,4+6,5+6,5+5,4+5,5+4
事件B为“两颗骰子的点数之和大干8”的概率P(B)=$\frac{10}{36}$=$\frac{5}{12}$,$\frac{\frac{5}{36}}{\frac{1}{3}}$
∴事件A发生时,事件B发生的概率P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{\frac{5}{36}}{\frac{1}{3}}$=$\frac{5}{12}$,
故答案为:$\frac{5}{12}$.
点评 本题考查条件概率,条件概率有两种做法,本题采用事件发生所包含的事件数之比来解出结果.

练习册系列答案
相关题目
1.若三条线段的长度分别为4、6、8,则用这三条线段( )
| A. | 能组成钝角三角形 | B. | 能组成锐角三角形 | ||
| C. | 能组成直角三角形 | D. | 不能组成三角形 |
8.已知函数f(x)的导函数为f'(x),且$f(1)=\frac{1}{2}$,不等式$f'(x)≤\frac{1}{x}+x$的解集为(0,1],则不等式$\frac{f(x)-lnx}{x^2}>\frac{1}{2}$的解集为( )
| A. | (0,1) | B. | (0,+∞) | C. | (1,+∞) | D. | (0,1)∪(1,+∞) |
5.某几何体的三视图如图所示,则该几何体的体积为( )
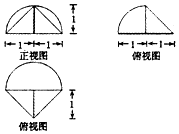

| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π+1}{3}$ | D. | $\frac{2π+1}{3}$ |