题目内容
7.与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1有共同的渐近线,且过点P(8,12)的双曲线方程为$\frac{{y}^{2}}{108}-\frac{{x}^{2}}{192}=1$.分析 利用双曲线的渐近线相同,设出双曲线方程,代入点的坐标,求解即可.
解答 解:与双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1有共同的渐近线,
且过点P(8,12)的双曲线方程设为:$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=m,(m≠0,m≠1)
可得:$\frac{144}{9}-\frac{64}{16}=m$,解得m=12,
所求的双曲线方程为:$\frac{{y}^{2}}{108}-\frac{{x}^{2}}{192}=1$.
故答案为:$\frac{{y}^{2}}{108}-\frac{{x}^{2}}{192}=1$.
点评 本题考查双曲线的简单性质以及双曲线方程的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.函数f(x)=ln(2x+1)-$\frac{3}{x}$在下列区间上单调递增的是( )
| A. | (-$\frac{1}{2}$,+∞) | B. | ($\frac{-3+\sqrt{3}}{2}$,+∞) | C. | ($\frac{-3+\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | (0,+∞) |
13.在△ABC中,三个内角A、B、C的对边分别是a,b,c,sinA>sinB则下列结论不一定成立的是( )
| A. | A>B | B. | sin2A>sin2B | C. | cos2A<cos2B | D. | a>b |
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ 2x+y-2≤0\\ y+2≥0\end{array}\right.$,则目标函数z=|x+3y|的最大值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
19.有一段“三段论”,推理是这样的:指数函数y=ax(a>0,a≠1)是增函数,因为$y={(\frac{1}{2})^x}$是指数函数,所以$y={(\frac{1}{2})^x}$是增函数,以上推理中( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
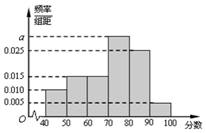 某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.