题目内容
1.若三条线段的长度分别为4、6、8,则用这三条线段( )| A. | 能组成钝角三角形 | B. | 能组成锐角三角形 | ||
| C. | 能组成直角三角形 | D. | 不能组成三角形 |
分析 利用余弦定理计算最大边所对的角的余弦值,根据计算结果进行判断.
解答 解:由两边之和大于第三边可知一定能组成三角形,
由正弦定理可知组成三角形的最大角所对的边长为8,
设最大角为α,由余弦定理得cosα=$\frac{{4}^{2}+{6}^{2}-{8}^{2}}{2×4×6}$=-$\frac{1}{4}$,
∴最大角α为钝角,
∴组成的三角形为钝角三角形.
故选:A.
点评 本题考查了余弦定理,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
6.某高中要从该校三个年级中各选取1名学生参加校外的一项知识问答活动,若高一、高二、高三年级分别有5,6,8个学生备选,则不同选法有( )
| A. | 19种 | B. | 38种 | C. | 120种 | D. | 240种 |
13.已知向量$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=(sinx+cosx,sinx-cosx)(x∈R),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x的取值集合为( )
| A. | {x|x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z} | B. | {x|x=kπ+$\frac{π}{8}$,k∈Z} | C. | {x|x=$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z} | D. | {x|x=kπ+$\frac{π}{4}$,k∈Z} |
10. 一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )
一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )
 一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )
一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )| A. | 24 | B. | 48 | C. | 72 | D. | 96 |
11.在100个球中有红球20个,从中抽取10个球进行分析,如果用分层抽样的方法对其进行抽样,则应抽取红球( )
| A. | 20 | B. | 10 | C. | 8 | D. | 2 |
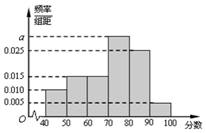 某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.