题目内容
8.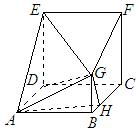 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH (1)求证:平面AGH⊥平面EFG
(2)若a=4,求三棱锥G-ADE的体积.
分析 (1)利用勾股定理逆定理证明GH⊥FG,根据CD⊥平面BCFG,CD∥EF得EF⊥GH,故而GH⊥平面EFG,于是平面AGH⊥平面EFG;
(2)根据GB∥CF∥DE得出BG∥平面ADE,故VG-ADE=VB-ADE=VE-ABD=VF-ABD.
解答  证明:(1)连接FH,
证明:(1)连接FH,
∵CD⊥BC,CD⊥CF,
∴CD⊥平面BCFG. 又∵GH?平面BCFG,
∴CD⊥GH. 又∵EF∥CD,
∴EF⊥GH,
∵AB=2BG=4BH=a,
∴GH=$\sqrt{B{G}^{2}+B{H}^{2}}$=$\frac{\sqrt{5}a}{4}$,FH=$\sqrt{F{C}^{2}+H{C}^{2}}$=$\frac{5a}{4}$,GF=$\sqrt{{a}^{2}+\frac{{a}^{2}}{4}}$=$\frac{\sqrt{5}a}{2}$,
∴FH2=FG2+GH2,
∴GH⊥FG.
又∵EF∩FG=F,EF?平面EFG,FG?平面EFG,
∴GH⊥平面EFG.又GH?平面AGH,
∴平面AGH⊥平面EFG.
解:(2)∵CF⊥平面ABCD,BG⊥平面ABCD,
∴CF∥BG,又∵ED∥CF,
∴BG∥ED,又BG?平面ADE,DE?平面ADE,
∴BG∥平面ADE,
∴VG-ADE=VB-ADE=VE-ABD=VF-ABD=$\frac{1}{3}$S△ABD•CF=$\frac{1}{3}×\frac{1}{2}×{4}^{2}×4$=$\frac{32}{3}$.
点评 本题考查了面面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
14.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
可用公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n(\overline x{)^2}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{({x_i}-\overline x{)^2}}}}$,$\widehat{a}$=$\overline y$-$\widehat{b}$$\overline x$.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
可用公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n(\overline x{)^2}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{({x_i}-\overline x{)^2}}}}$,$\widehat{a}$=$\overline y$-$\widehat{b}$$\overline x$.
19.一个三角形的三个内角A,B,C成等差数列,则cosB=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
16.若复数z满足(3-4i)z=|4+3i|,则$\overline{z}$的虚部为( )
| A. | $-\frac{4}{5}i$ | B. | $-\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{5}i$ |