题目内容
16.若复数z满足(3-4i)z=|4+3i|,则$\overline{z}$的虚部为( )| A. | $-\frac{4}{5}i$ | B. | $-\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{5}i$ |
分析 把已知等式变形,再由复数代数形式的乘除运算化简求得z,进一步得到$\overline{z}$得答案.
解答 解:由(3-4i)z=|4+3i|,得
z=$\frac{|4+3i|}{3-4i}=\frac{5}{3-4i}=\frac{5(3+4i)}{(3-4i)(3+4i)}=\frac{3}{5}+\frac{4}{5}i$,
∴$\overline{z}=\frac{3}{5}-\frac{4}{5}i$.
∴$\overline{z}$的虚部为$-\frac{4}{5}$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.设f(x)=(2x+5)6,在函数f'(x)中x3的系数是( )
| A. | 2000 | B. | 12000 | C. | 24000 | D. | 非以上答案 |
4.函数f(x)=$\frac{{x}^{2}}{x-1}$(x>1)的最小值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图,E,F,G分别是四面体ABCD的棱BC、CD、DA的中点,则此四面体与过E,F,G的截面平行的棱的条数是2.
如图,E,F,G分别是四面体ABCD的棱BC、CD、DA的中点,则此四面体与过E,F,G的截面平行的棱的条数是2.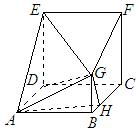 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH 


