题目内容

证明不等式：如果a，b都是正数，且a≠b，求证：
a
b
+
b
a
＞
a
+
b
．
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：利用作差法，即可证明结论．
解答： 证明：
a
b
+
b
a
-（
a
+
b
）=（a-b）（
1
b
-
1
a
）=
(
a
+
b
)(
a
-
b
)2
ab
，
∵a，b都是正数，且a≠b，
∴
(
a
+
b
)(
a
-
b
)2
ab
＞0，
∴
a
b
+
b
a
＞
a
+
b
．
点评：利用作差法，正确因式分解是关键．
练习册系列答案
相关题目
如果命题“p且q”是假命题，“非p”是真命题，那么（　　）
A、命题p 一定是真命题
B、命题q 一定是真命题
C、命题q 可以是真命题也可以是假命题
D、命题q 一定是假命题
设f（x+2）=2x+1，则f（2）等于（　　）
A、1B、2C、3D、4
某几何体的三视图如图所示，则该几何体是（　　）
A、圆柱B、圆锥
C、三棱柱D、三棱锥
某中学高一（2）班甲、乙两名同学自入高中以来每场数学考试成绩情况如下：
甲同学得分：95，81，75，91，86，89，71，65，76，88，94，110；
乙同学得分：83，86，93，99，88，103，98，114，98，79，101，107．
画出两人数学成绩的茎叶图，并根据茎叶图对两人的成绩进行比较．
下面是水稻产量与施化肥量的一组观测数据（单位：千克/亩）：
施化肥量15202530354045
水稻产量320330360410460470480
（1）将上述数据制成散点图；
（2）你能从散点图中发现施化肥量与水稻产量近似成什么关系吗？水稻产量会一直随施化肥量的增加而增长吗？
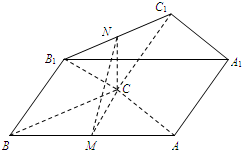如图，三棱柱ABC-A1B1C1中，M，N分别为AB，B1C1的中点．
（1）求证：MN∥平面AA1C1C；
（2）若CC1=CB1，CA=CB，平面CC1B1B⊥平面ABC，求证：AB⊥平面CMN．
如图，在y轴的正半轴上依次有点A1、A2、…、An，其中点A1（0，1）、A2（0，10），且|An-1An|=3|AnAn+1|（n=2，3，4，…），在射线y=x（x≥0）上依次有点B1、B2、…、Bn，点B1的坐标为（3，3），且|OBn|=|OBn-1|+2
2
（n=2，3，4，…）．
（1）求点An、Bn的坐标（用含n的式子表示）；
（2）设四边形AnBnBn+1An+1面积为Sn，求数列{Sn}的通项公式．
若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则此几何体的体积等于（　　）
A、30B、12C、24D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网