题目内容
若数集M满足条件:若a∈M,则
∈M(a≠0,a≠±1),则集合M中至少有几个元素?
| 1+a |
| 1-a |
考点:元素与集合关系的判断
专题:计算题,集合
分析:选由题意推出集合M中的元素,注意验证元素互异.
解答:
解:由a∈M,则
∈M知,
=-
∈M,
=
∈M,
=a∈M.
又∵a,
,-
,
互不相等,
故集合M中至少有4个元素.
| 1+a |
| 1-a |
1+
| ||
1-
|
| 1 |
| a |
1-
| ||
1+
|
| a-1 |
| a+1 |
1+
| ||
1-
|
又∵a,
| 1+a |
| 1-a |
| 1 |
| a |
| a-1 |
| a+1 |
故集合M中至少有4个元素.
点评:本题考查了集合中元素的个数及元素与集合的关系.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
设命题p:ax2+2ax+1>0的解集是实数集R;q:0<a<1,则p是q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某几何体的三视图如图所示,则该几何体是( )


| A、圆柱 | B、圆锥 |
| C、三棱柱 | D、三棱锥 |
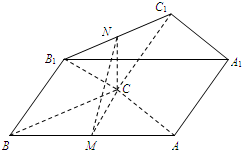 如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点. 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题: 如图,在y轴的正半轴上依次有点A1、A2、…、An,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1、B2、…、Bn,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2
如图,在y轴的正半轴上依次有点A1、A2、…、An,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1、B2、…、Bn,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2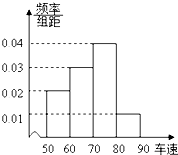 某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )
某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )