题目内容
19.给出下列等式:$\sqrt{2}$=2cos$\frac{π}{4}$,
$\sqrt{2+\sqrt{2}}$=2cos$\frac{π}{8}$,
$\sqrt{2+\sqrt{2+\sqrt{2}}}$=2cos$\frac{π}{16}$
…
请从中归纳出第n(n∈N*)个等式:$\sqrt{2+…+\sqrt{2+\sqrt{2}}}$=2cos$\frac{π}{{2}^{n+1}}$.
分析 通过已知的三个等式,找出规律,归纳出第n个等式即可.
解答 解:因为$\sqrt{2}$=2cos$\frac{π}{4}$,
$\sqrt{2+\sqrt{2}}$=2cos$\frac{π}{8}$,
$\sqrt{2+\sqrt{2+\sqrt{2}}}$=2cos$\frac{π}{16}$
…,
等式的右边系数是2,角是等比数列,公比为$\frac{1}{2}$角的余弦值,角满足:$\frac{π}{{2}^{n+1}}$,
所以$\sqrt{2+…+\sqrt{2+\sqrt{2}}}$=2cos$\frac{π}{{2}^{n+1}}$.
故答案为:2cos$\frac{π}{{2}^{n+1}}$.
点评 本题考查归纳推理,注意已知表达式的特征是解题的关键.

练习册系列答案
相关题目
10.“ln(x+2)<0”是“x<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.运行如图所示的算法框图,输出的结果是( )
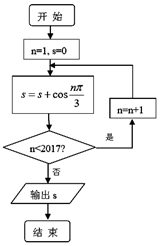

| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $-\frac{3}{2}$ |
11.(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(3,0)+f(0,3)=( )
| A. | 9 | B. | 16 | C. | 18 | D. | 24 |
13.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}-ax-5,(x≤1)\\ \frac{a}{x}(x>1)\end{array}$是R上的增函数,则a的取值范围是( )
| A. | {a|-3≤a<0} | B. | {a|a≤-2} | C. | {a|a<0} | D. | {a|-3≤a≤-2} |