题目内容
14.运行如图所示的算法框图,输出的结果是( )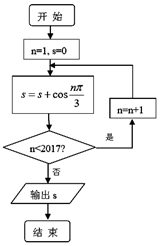
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $-\frac{3}{2}$ |
分析 根据所给的程序框图,写出循环过程中前几次循环的结果,列举出前几次的结果,得出以6为周期进行循环,2017=6×336+1,即可得出输出的结果.
解答 解:由程序框图知,
当n=1时,s=cos$\frac{π}{3}$=$\frac{1}{2}$,
当n=2时,s=$\frac{1}{2}$+cos$\frac{2π}{3}$=0,
当n=3时,s=0-1=-1
当n=4时,s=-1-$\frac{1}{2}$=-$\frac{3}{2}$,
当n=5时,s=-1
当n=6时,s=0,
以6为周期进行循环,2017=6×336+1,故输出的结果是$\frac{1}{2}$,
故选C.
点评 本题考查循环结构,本题解题的关键是看出循环过程中的前几项,有必要写出前几项看出结果,对于比较多的项,要找出规律,本题是一个基础题.

练习册系列答案
相关题目
4.在区间[0,8]上随机取一个x的值,执行如图的程序框图,则输出的y≥3的概率为( )


| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
5.已知A为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点,B为点A关于原点的对称点,F为椭圆的左焦点,且AF⊥BF,若∠ABF∈[$\frac{π}{12}$,$\frac{π}{4}$],则该椭圆离心率的取值范围为( )
| A. | [0,$\frac{\sqrt{2}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [0,$\frac{\sqrt{6}}{3}$] | D. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{3}$] |
2.已知集合M={-1,0,1,2,3},N={x|x2-2x>0},则M∩N=( )
| A. | {3} | B. | {2,3} | C. | {-1,3} | D. | {0,1,2} |
6.已知函数$f(x)=\left\{\begin{array}{l}-{x^2}+4x,x≤2\\{log_2}x-a,x>2\end{array}\right.$有两个不同的零点,则实数a的取值范围是( )
| A. | [-1,0) | B. | (1,2] | C. | (1,+∞) | D. | (2,+∞) |
8.函数$f(x)=tan(2x-\frac{π}{6})$的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |