题目内容
19.若一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,则原平面图形的周长为( )| A. | 4+$\sqrt{2}$+$\sqrt{6}$ | B. | 3+$\sqrt{2}$+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
分析 根据题意画出图形,结合图形得出原来的平面图形的上底与下底、高,从而求出它的周长.
解答 解:根据题意,画出图形,如图所示;

原来的平面图形上底是1,下底是1+$\sqrt{2}$,高是2的直角梯形,
它的周长是1+2+(1+$\sqrt{2}$)+$\sqrt{{2}^{2}{+(\sqrt{2})}^{2}}$=4+$\sqrt{2}$+$\sqrt{6}$.
故选:A.
点评 本题考查了平面图形的直观图的画法与应用问题,是基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13.已知实数a,b满足(a+i)(1-i)=3+bi(i为虚数单位),记z=a+bi,则|z|是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 5 | D. | 25 |
10.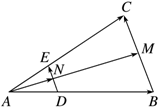 如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )
如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )
 如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )
如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )| A. | $\frac{1}{2}$($\overrightarrow a$+$\overrightarrow{b}$) | B. | $\frac{1}{3}$( $\overrightarrow a$+$\overrightarrow{b}$) | C. | $\frac{1}{6}$( $\overrightarrow a$+$\overrightarrow{b}$) | D. | $\frac{1}{8}$( $\overrightarrow a$+$\overrightarrow{b}$) |
7.若某几何体的三视图(单位:cm)如图所示,则此几何体的侧面积等于( )
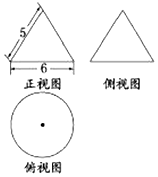

| A. | 12πcm2 | B. | 15πcm2 | C. | 24πcm2 | D. | 30πcm2 |
9.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分.两人4局的得分情况如下:
(1)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求x+y的值;
(2)如果x=6,y=10,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为a,b,求a>b的概率;
(3)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出x的所有可能取值.(结论不要求证明)
| 甲 | 6 | 6 | 9 | 9 |
| 乙 | 7 | 9 | x | y |
(2)如果x=6,y=10,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为a,b,求a>b的概率;
(3)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出x的所有可能取值.(结论不要求证明)
 把正整数按一定的规律排成如图所示的三角形数阵.设aij(i,j∈N*)是位于数阵中从上向下数第i行,从左向右数第j列的数,例如:a43=10,若aij=173,则i+j=11.
把正整数按一定的规律排成如图所示的三角形数阵.设aij(i,j∈N*)是位于数阵中从上向下数第i行,从左向右数第j列的数,例如:a43=10,若aij=173,则i+j=11.