题目内容
11.在△ABC中,角A,B,C的对边分别为a,b,c,已知△ABC的外接圆半径R=$\sqrt{2}$,且tanB+tanC=$\frac{\sqrt{2}sinA}{cosC}$(1)求B和b的值;
(2)求△ABC面积的最大值.
分析 (1)由已知利用同角三角函数基本关系式,两角和的正弦函数公式,三角形内角和定理可求cosB=$\frac{\sqrt{2}}{2}$,可得B的值,进而由正弦定理可得b的值,
(2)由余弦定理和基本不等式可求出ac≤2(2+$\sqrt{2}$),再根据三角形的面积公式计算即可
解答 解:(1)∵tanB+tanC=$\frac{\sqrt{2}sinA}{cosC}$,
∴$\frac{sinB}{cosB}$+$\frac{sinC}{cosC}$=$\frac{\sqrt{2}sinA}{cosC}$,
∴sinBcosC+cosBsinC=$\sqrt{2}$sinAcosB,
即sin(B+C)=$\sqrt{2}$sinAcosB,
∵A+B+C=π,
∴sinA=$\sqrt{2}$sinAcosB
∵sinA≠0,
∴cosB=$\frac{\sqrt{2}}{2}$,
∴B=$\frac{π}{4}$.
又∵△ABC的外接圆半径为R=$\sqrt{2}$,
∴由正弦定理$\frac{b}{sinB}$=2R,可得:b=2×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2.
(2)由余弦定理的b=a2+c2-2accosB,
∴4=a2+c2-$\sqrt{2}$ac,
由基本不等式,得4=a2+c2-$\sqrt{2}$ac≥2ac-$\sqrt{2}$ac,
∴ac≤$\frac{4}{2-\sqrt{2}}$=2(2+$\sqrt{2}$),
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{\sqrt{2}}{4}$ac≤$\frac{\sqrt{2}}{4}$×2(2+$\sqrt{2}$)=1+$\sqrt{2}$,
故△ABC面积的最大值1+$\sqrt{2}$.
点评 本题主要考查了同角三角函数基本关系式,两角和的正弦函数公式,三角形内角和定理,正弦定理,三角形的面积公式和基本不等式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

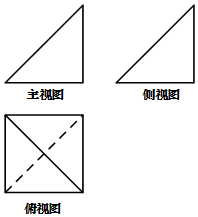 某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )
某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | 32 |
| A. | 4+$\sqrt{2}$+$\sqrt{6}$ | B. | 3+$\sqrt{2}$+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
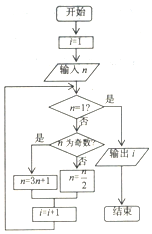 20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )
20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )