题目内容
14.若圆(x-3)2+(y+5)2=r2上恰有3个点到直线4x-3y=2的距离等于1,则半径r的值为6.分析 由题意画出图形,把圆(x-3)2+(y+5)2=r2上恰有3个点到直线4x-3y=2的距离等于1转化为圆心C(3,-5)到直线4x-3y=2的距离等于r-1.再由点到直线的距离公式列式求得r值.
解答 解:如图,
要使圆(x-3)2+(y+5)2=r2上恰有3个点到直线4x-3y=2的距离等于1,
则圆心C(3,-5)到直线4x-3y=2的距离等于r-1.
由点到直线的距离公式得d=$\frac{|4×3-3×(-5)-2|}{\sqrt{{3}^{2}+(-5)^{2}}}=r-1$,解得r=6.
故答案为:6.
点评 本题考查直线与圆位置关系的应用,考查点到直线的距离公式,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
5.设随机变量X的分布列为P(X=k)=$\frac{k}{25}$,k=1,2,3,4,5,则P($\frac{1}{2}$<X<$\frac{5}{2}$)等于( )
| A. | $\frac{2}{15}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{15}$ |
2.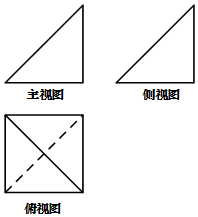 某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )
某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )
 某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )
某空间几何体的三视图如图所示,图中主视图和侧视图是两个全等的等腰直角三角形,腰长为4,俯视图中的四边形为正方形,则这个几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | 32 |
19.若一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,则原平面图形的周长为( )
| A. | 4+$\sqrt{2}$+$\sqrt{6}$ | B. | 3+$\sqrt{2}$+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
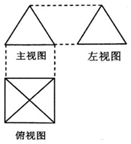 如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.
如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.