题目内容
9.已知函数$f(x)=lnx+\frac{1}{2x}$.(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设g(x)=f(x)-m.若函数g(x)在区间$[{\frac{1}{e}\;,\;1}]$上有且只有一个零点,求实数m的取值范围(注:e为自然对数的底数).
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)问题转化为m=f(x)在区间$[{\frac{1}{e}\;,\;1}]$上有且只有一个交点,求出f(x)在区间$[{\frac{1}{e}\;,\;1}]$上的范围,求出m的范围即可.
解答 解:(Ⅰ)f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$-$\frac{1}{{2x}^{2}}$=$\frac{2x-1}{{2x}^{2}}$,
令f′(x)>0,解得:x>$\frac{1}{2}$,
令f′(x)<0,解得:0<x<$\frac{1}{2}$,
∴f(x)在(0,$\frac{1}{2}$)递减,在($\frac{1}{2}$,+∞)递增;
(Ⅱ)若函数g(x)在区间$[{\frac{1}{e}\;,\;1}]$上有且只有一个零点,
即m=f(x)在区间$[{\frac{1}{e}\;,\;1}]$上有且只有一个交点,
由(Ⅰ)f(x)在[$\frac{1}{e}$,$\frac{1}{2}$)递减,在($\frac{1}{2}$,1]递增,
故f(x)的最小值是f($\frac{1}{2}$)=1-ln2,而f($\frac{1}{e}$)=$\frac{e}{2}$-1<f(1)=$\frac{1}{2}$,
故$\frac{e}{2}$-1<m≤$\frac{1}{2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
1.已知函数f(x)=loga(6-ax)在(-3,2)上是减函数,则a的取值范围是( )
| A. | (0,3) | B. | (1,3] | C. | (1,3) | D. | [3,+∞) |
18.已知椭圆C1和抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于表中:
(1)求椭圆C1和抛物线C2的标准方程;
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,点P(4,0),设$\overrightarrow{FA}=λ\overrightarrow{FB},λ∈[{-2,-1}]$,求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时,直线l的斜率.
| x | $-\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | $-\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,点P(4,0),设$\overrightarrow{FA}=λ\overrightarrow{FB},λ∈[{-2,-1}]$,求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时,直线l的斜率.
19.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾天气的主要原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
(Ⅰ)分别求这两年样本数据的中位数和平均值,并以此推断2016年11月~12月的空气质量是否比2015年同期有所提高?
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.
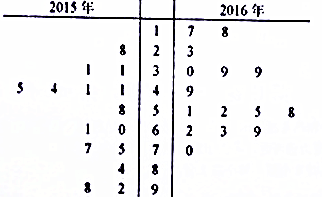
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k<75 | 二级 |
| k>75 | 超标 |
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.

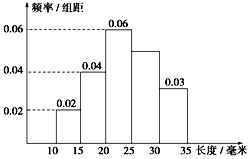 对一批零件的长度(单位:mm)进行抽样检测,检测结果的频率分布直方图如图所示.根据标准,零件长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.
对一批零件的长度(单位:mm)进行抽样检测,检测结果的频率分布直方图如图所示.根据标准,零件长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品. 国庆期间,高速公路堵车现象经常发生.某调查公司为了了解车速,在赣州西收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(km/h))分成六段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后,得到如图的频率分布直方图.
国庆期间,高速公路堵车现象经常发生.某调查公司为了了解车速,在赣州西收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(km/h))分成六段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后,得到如图的频率分布直方图.