��Ŀ����
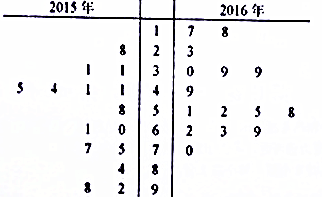
19��PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ��Ϊ����ο���������γ�������������Ҫԭ��֮һ��PM2.5�վ�ֵԽС����������Խ��.2012��2��29�գ����һ����������ġ���������������������������������ص�����������ػ����������˻���������������ɽ�л����ִ�����2015��11�¡�12�º�2016��11�¡�12�µ�PM2.5��������и������ȡ15�����������������Ч�������������羥Ҷͼ��ʾ��ʮλΪ������λΪҶ��
| PM2.5�վ�ֵk���ˣ� | ���������ȼ� |
| k��35 | һ�� |
| 35��k��75 | ���� |
| k��75 | ���� |
������2016������������������ȡ3�죬��X��ʾ�鵽��������Ϊһ������������X�ķֲ�����������
���� ��1������ƽ�������㹫ʽ���ɵó���
��2��2016���15����������4���������Ϊһ������X�����п���ȡֵ��0��1��2��3������P��X=k��=$\frac{{∁}_{4}^{3-k}{∁}_{11}^{k}}{{∁}_{15}^{3}}$���ɵó���
��� �⣺��1��2015�����ݵ���λ����58��ƽ������$\frac{28+31+31+41+41+44+45+58+60+61+75+77+84+92+98}{15}$��57.3
2016�����ݵ���λ����51��ƽ������$\frac{17+18+23+30+39+39+49+51+52+55+58+62+63+69+70}{15}$
��46.3��
2016��11�¡�12�±�2015��11�¡�12�µĿ�����������ߣ�
��2��2016���15����������4���������Ϊһ������X�����п���ȡֵ��0��1��2��3��
����P��X=k��=$\frac{{∁}_{4}^{3-k}{∁}_{11}^{k}}{{∁}_{15}^{3}}$�ɵã�
P��X=0��=$\frac{33}{91}$��P��X=1��=$\frac{44}{91}$��P��X=2��=$\frac{66}{455}$��P��X=3��=$\frac{4}{455}$��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{33}{91}$ | $\frac{44}{91}$ | $\frac{66}{455}$ | $\frac{4}{455}$ |
���� ���⿼��ͳ�ƺ���ɢ����������ķֲ�������ѧ�������㹫ʽ��������������������������������е��⣮

��ϰ��ϵ�д�
 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
�����Ŀ
7����֪����$f��x��=lg\frac{1+ax}{1-2x}$�Ƕ����ڣ�-b��b���ϵ��溯������a��b��R��a��-2������ab��ȡֵ��Χ�ǣ�������
| A�� | $��{1��\sqrt{2}}]$ | B�� | $��{0��\sqrt{2}}]$ | C�� | $��{1��\sqrt{2}}��$ | D�� | $��{0��\sqrt{2}}��$ |