题目内容
1.已知函数f(x)=loga(6-ax)在(-3,2)上是减函数,则a的取值范围是( )| A. | (0,3) | B. | (1,3] | C. | (1,3) | D. | [3,+∞) |
分析 由已知中f(x)=loga(6-ax)在(-3,2)上为减函数,结合底数的范围,可得内函数为减函数,则外函数必为增函数,再由真数必为正,可得a的取值范围.
解答 解:若函数f(x)=loga(6-ax)在(-3,2)上为减函数,
则$\left\{\begin{array}{l}{a>1}\\{6-2a≥0}\end{array}\right.$
解得:a∈(1,3]
故选B.
点评 本题考查的知识点是复合函数的单调性,其中根据已知分析出内函数为减函数,则外函数必为增函数,是解答的关键

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
16.在△ABC中,根据下列条件解三角形,其中有两解的是( )
| A. | b=7,c=3,C=30° | B. | a=20,b=30,C=30° | C. | b=4,c=2$\sqrt{3}$,C=60° | D. | b=5,c=4,C=45° |
6.经过直线2x-y=0与直线x+y-6=0的交点,且与直线2x+y-1=0垂直的直线方程是( )
| A. | x-2y+6=0 | B. | x-2y-6=0 | C. | x+2y-10=0 | D. | x+2y-8=0 |
13.P(3,y)为α终边上一点,$cosα=\frac{3}{5}$,则y=( )
| A. | -3 | B. | 4 | C. | ±3 | D. | ±4 |
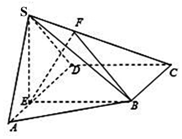 如图,在四棱锥S-ABCD中,平面SAD⊥底面ABCD,$∠SAD=\frac{π}{3}$,在AD边上取一点E,使得BCDE为矩形,SA=2AE=DE=2.
如图,在四棱锥S-ABCD中,平面SAD⊥底面ABCD,$∠SAD=\frac{π}{3}$,在AD边上取一点E,使得BCDE为矩形,SA=2AE=DE=2.