题目内容

18．如图，点E是正方形ABCD的边CD的中点，若$\overrightarrow{AE}$•$\overrightarrow{DB}$=-2，则$\overrightarrow{AE}$•$\overrightarrow{BE}$的值为3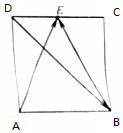

分析 建立直角坐标系，设出正方形的边长，利用向量的数量积求出边长，然后求解数量积的值．

解答 解：以A为坐标原点，AB为x轴，AD为y轴，设正方形的边长为2a，
则：E（a，2a），B（2a，0），D（0，2a）
可得：$\overrightarrow{AE}$=（a，2a），$\overrightarrow{DB}$=（2a，-2a）．
若$\overrightarrow{AE}$•$\overrightarrow{DB}$=-2，可得2a2-4a2=-2，解得a=1，
$\overrightarrow{BE}$=（-1，2），$\overrightarrow{AE}$=（1，2），
则$\overrightarrow{AE}$•$\overrightarrow{BE}$的值：-1+4=3．
故答案为：3．

点评 本题考查平面向量的数量积的运算，考查转化思想以及计算能力．

练习册系列答案
相关题目
8．△ABC的两边长为2，3，其夹角的余弦为$\frac{1}{3}$，则其外接圆半径为（　　）
A．$\frac{{9\sqrt{2}}}{2}$B．$\frac{{9\sqrt{2}}}{4}$C．$\frac{{9\sqrt{2}}}{8}$D．$\frac{{2\sqrt{2}}}{9}$
9．设实数x，y满足$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{y≥x}\end{array}\right.$，则x+2y的最小值为（　　）
A．1.5B．2C．5D．6
6．已知函数f（x）=|x-3|+|x-1|，若存在x∈R，使f（x）≥2a，则实数a的取值范围是（-∞，1]．
13．函数f（x）=3sin（3x+$\frac{π}{4}$）的最小正周期为$\frac{2π}{3}$．
3．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的最下正周期为π，且点P（$\frac{π}{6}$，2）是该函数图象的一个人最高点．
（1）求函数f（x）的解析式；
（2）若x∈[-$\frac{π}{2}$，0]，求函数y=f（x）的值域；
（3）把函数y=f（x）的图线向右平移θ（0＜θ＜$\frac{π}{2}$）个单位，得到函数y=g（x）在[0，$\frac{π}{4}$]上是单调增函数，求θ的取值范围．
10．设α，β是两个平面，m，n是两条直线，有下列四个命题：
（1）如果m⊥n，m⊥α，n∥β，那么α⊥β．
（2）如果m⊥α，n∥α，那么m⊥n．
（3）如果α∥β，m?α，那么m∥β．
其中正确命题的个数（　　）
A．0B．1C．2D．3
7．已知圆的方程为（x-1）2+（y-1）2=9，P（2，2）是该圆内一点，过点P的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积是6$\sqrt{7}$．
8．若圆锥的侧面展开图是圆心角为90°的扇形，则这个圆锥的侧面积与底面积的比是4：1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网