题目内容

8．若方程sin2x+2sinx+a=0有解，则实数a的取值范围是（　　）
A．[-3，1]B．（-∞，1]C．[1，+∞）D．[-1，1]

分析 用sinx表示a，进而二次函数的性质和sinx的范围确定a的范围．

解答 解：对方程等价变换得a=-sin2x-2sinx=-sin2x-2sinx-1+1=-（sinx+1）2+1，
∵-1≤sinx≤1，
∴-3≤a≤1
故选：A．

点评 本题主要考查了二次函数的性质，三角函数的最值问题．解题的关键是转化成二次函数的问题，利用二次函数的性质来解决．

练习册系列答案
相关题目
7．已知函数f（x）=$\frac{{{e^x}-m}}{{{e^x}+1}}$+mx是定义在R上的奇函数，则实数m=1．
8．若a＞b＞0，c＜d＜0，则一定有（　　）
A．ac＞bdB．ac＜bdC．ad＜bcD．ad＞bc
5．棱长为2的正方体的顶点都在同一个球面上，则球的表面积是（　　）
A．8πB．12πC．16πD．20π
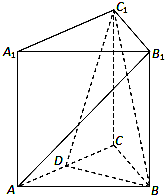3．三棱ABC-A1B1C1，A1A⊥底面ABC，且△ABC为正三角形，且，D为AC中点．
（1）求证：平面BC1D⊥平面AA1CC1
（2）若AA1=AB=2，求点A到面BC1D的距离．
13．在平面直角坐标系xOy中，以坐标原点O为极点，x轴的非负半轴为极轴，建立极坐标系．曲线C的极坐标方程是ρ=4cosθ（0$≤θ≤\frac{π}{2}$），直线l的参数方程是$\left\{\begin{array}{l}{x=-3+tcos\frac{π}{6}}\\{y=tsin\frac{π}{6}}\end{array}\right.$（t为参数）．
（1）求直线l的直角坐标方程和曲线C的参数方程；
（2）求曲线C上的动点M到直线l的距离的范围．
20．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，右顶点A是抛物线y2=8x的焦点．
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在过点P（0，$\frac{5}{3}$）的直线l与椭圆交于M，N两个不同的点，且使$\overrightarrow{QM}$=4$\overline{QN}$-3$\overline{QP}$成立（Q为直线l外的一点）？若存在，求出l的方程；若不存在，说明理由．
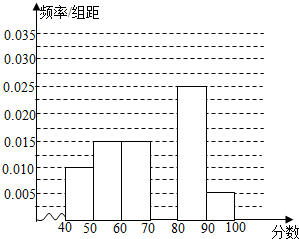17．某校参加高一年级期中考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[40，50），[50，60），…，[90，100）后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：
（Ⅰ）求分数在[70，80）内的频率；并补全频率分布直方图；
（Ⅱ）求在[60，70），[70，80）分数段上各有多少人？
（Ⅲ）用分层抽样方法在分数段[60，80）的学生中抽取一个容量为6的样本．将该样本看成一个总体，从中任取2人，求至多有一人在分数段[60，80）的概率．
18．在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．在极坐标系中，设点P为曲线C1：ρ=2cosθ上的任意一点，点Q在射线OP上，且满足|OP|•|OQ|=6，记Q点的轨迹为C2．
（1）求曲线C2的直角坐标方程；
（2）直线l：θ=$\frac{π}{3}$分别交C1与C2交于A，B两点，求|AB|．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网