题目内容
7.直线x-y-1=0与圆(x-1)2+(y-2)2=4相交于A、B两点,则弦AB的长为$2\sqrt{2}$.分析 根据已知中圆的标准方程和直线的一般方程,代入圆的弦长公式,可得答案.
解答 解:圆(x-1)2+(y-2)2=4的圆心坐标为(1,2),半径r=2,
圆心到直线x-y-1=0的距离d=$\sqrt{2}$,
故弦AB=2$\sqrt{{r}^{2}-{d}^{2}}$=$2\sqrt{2}$,
故答案为:$2\sqrt{2}$
点评 本题考查的知识点是直线与圆的位置关系,熟练掌握圆的弦长公式,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列四个图形中,能表示函数y=f(x)的是( )
| A. | 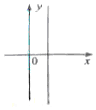 | B. | 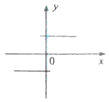 | C. | 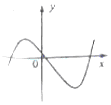 | D. | 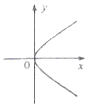 |
8.已知椭圆的中心在原点,离心率e=$\frac{1}{2}$,且它的一个焦点与抛物线x2=-4y的焦点重合,则此椭圆的方程为( )
| A. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ | B. | $\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$ | C. | ${x}^{2}+\frac{{y}^{2}}{2}=1$ | D. | $\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$ |
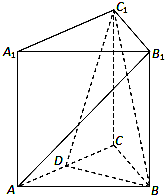 三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.
三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.