题目内容
3.已知函数f(x)=x2+1,g(x)=f(f(x))-2λf(x),若函数g(x)在区间[-2,-1]为增函数,则λ的取值范围为(-∞,2].分析 求出函数g(x)的解析式,通过换元,得到g(x)=g(t)=t2-2λt+1,求出函数的对称轴,根据二次函数的性质求出λ的范围即可.
解答 解:∵f(x)=x2+1,
∴g(x)=f(f(x))-2λf(x)=(x2+1)2+1-2λ(x2+1),
令t=x2+1,x∈[-2,-1],
则t∈[2,5],
故g(x)=g(t)=t2-2λt+1,
对称轴是x=λ,
若函数g(x)在区间[-2,-1]为增函数,
则λ≤2,
故答案为:(-∞,2].
点评 本题考查了二次函数的性质,考查函数的单调性问题,是一道中档题.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
11.若${(x-2)^5}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}$,则a1+a2+a3+a4+a5=( )
| A. | -1 | B. | -31 | C. | -33 | D. | 31 |
12.在△ABC中,内角A,B,C所对的边分别是a,b,c,若c2=(a-b)2+6,C=$\frac{π}{3}$,则△ABC的面积是( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{9\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |
13.函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( )
| A. | 在点x0处的斜率 | |
| B. | 在点(x0,f(x0))处的切线与x轴所夹的锐角的正切值 | |
| C. | 曲线y=f(x)在点(x0,f(x0))处切线的斜率 | |
| D. | 点(x0,f(x0))与点(0,0)连线的斜率 |
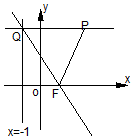 如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.
如图在直角坐标系xOy中,过动点P的直线与直线l:x=-1垂直,垂足为Q,点F(1,0)满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$.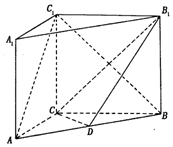 如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,$A{A_1}=AC=CB=\frac{{\sqrt{2}}}{2}AB$
如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,$A{A_1}=AC=CB=\frac{{\sqrt{2}}}{2}AB$