题目内容
12.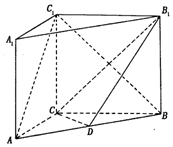 如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,$A{A_1}=AC=CB=\frac{{\sqrt{2}}}{2}AB$
如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,$A{A_1}=AC=CB=\frac{{\sqrt{2}}}{2}AB$(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角D-CB1-B的平面角的余弦值.
分析 (Ⅰ)证明AC⊥平面BCC1,即可证明:AC⊥BC1;
(Ⅱ)取BC中点E,过D作DF⊥B1C于F,连接EF,证明∠EFD是二面角D-CB1-B的平面角,即可求二面角D-CB1-B的平面角的余弦值.
解答 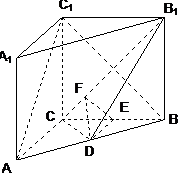 (Ⅰ)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
(Ⅰ)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∵AC2+BC2=AB2
∴AC⊥BC,
又 AC⊥C1C,且BC∩C1C=C
∴AC⊥平面BCC1,又BC1?平面BCC1
∴AC⊥BC1 …(4分)
(Ⅱ)解:取BC中点E,过D作DF⊥B1C于F,连接EF …(5分)
∵D是AB中点,
∴DE∥AC,又AC⊥平面BB1C1C,
∴DE⊥平面BB1C1C,
又∵EF?平面BB1C1C,BC1?平面BB1C1C
∴DE⊥EF.
∴BC1⊥DE
又∵DF⊥BC1 且DE∩DF=D
∴B1C⊥平面DEF,EF?平面DEF …(7分)
∴B1C⊥EF
又∵DF⊥B1C,
∴∠EFD是二面角D-CB1-B的平面角 …(9分)
∵AC=BC=$\sqrt{2}$=AA1
∴在△DEF中,DE⊥EF,$DE=\frac{{\sqrt{2}}}{2}$,$EF=\frac{1}{2}$,$DF=\frac{{\sqrt{3}}}{2}$
∴$cos∠EFD=\frac{EF}{DF}=\frac{{\sqrt{3}}}{3}$…(11分)
∴二面角D-CB1-B余弦值为$\frac{{\sqrt{3}}}{3}$…(12分)
点评 本题考查空间中直线与平面之间的垂直关系,考查面与面的夹角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)是定义在R上的偶函数,x<0时,f(x)=x3,那么f(2)的值是( )
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
7.已知抛物线C:y2=2px(p>0)上一点(5,m)到焦点的距离为6,P,Q分别为抛物线C与圆M:(x-6)2+y2=1上的动点,当|PQ|取得最小值时,向量$\overrightarrow{PQ}$在x轴正方向上的投影为( )
| A. | 2-$\frac{{\sqrt{5}}}{5}$ | B. | 2$\sqrt{5}$-1 | C. | 1-$\frac{{\sqrt{21}}}{21}$ | D. | $\sqrt{21}$-1 |
17.向量$\overrightarrow{OA}$对应的复数为1+4i,向量$\overrightarrow{OB}$对应的复数为-3+2i,则向量$\overrightarrow{OA}+\overrightarrow{OB}$对应的复数为( )
| A. | 4+2i | B. | -4-2i | C. | -2+4i | D. | -2+6i |
4.下列函数中,周期是$\frac{π}{2}$的偶函数是( )
| A. | y=sin4x | B. | .y=tan2x | C. | y=cos22x-sin22x | D. | y=cos2x |
1.已知三次函数f(x)=x3+ax2+7ax在 (-∞,+∞)是增函数,则a的取值范围是( )
| A. | 0≤a≤21 | B. | a=0或a=7 | C. | a<0或a>21 | D. | a=0或a=21 |
2.已知直线x-y+2=0与圆C:(x-3)2+(y-3)2=4交于点A,B,过弦AB的中点的直径为MN,则四边形AMBN的面积为( )
| A. | $8\sqrt{2}$ | B. | 8 | C. | $4\sqrt{2}$ | D. | 4 |