题目内容
20.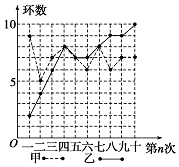 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:(Ⅰ)请填写表:
| 平均数 | 方差 | 命中9环及9环以上的次数 | |
| 甲 | |||
| 乙 |
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
分析 (Ⅰ)由折线图,求出甲射击10次中靶环数和乙射击10次中靶环数,由此能求出结果.
(Ⅱ)①由平均数相同,$S_甲^2$<$S_乙^2$,知甲成绩比乙稳定.
②由平均数相同,命中9环及9环以上的次数甲比乙少,知乙成绩比甲好些.
③乙处于上升势头,从第四次以后就没有比甲少的情况发生,乙较有潜力.
解答 【解析】(Ⅰ)由折线图,知
甲射击10次中靶环数分别为:9,5,7,8,7,6,8,6,7,7.
将它们由小到大重排为:5,6,6,7,7,7,7,8,8,9.
乙射击10次中靶环数分别为:2,4,6,8,7,7,8,9,9,10.
也将它们由小到大重排为:2,4,6,7,7,8,8,9,9,10.
(Ⅰ)${\overline x_甲}$=$\frac{1}{10}×(5+6×2+7×4+8×2+9)=\frac{70}{10}=7$(环),
${\overline x_乙}$=$\frac{1}{10}×(2+4+6+7×2+8×2+9×2+10)=\frac{70}{10}=7$(环) …2分
$S_甲^2$=$\frac{1}{10}×({(5-7)^2}+{(6-7)^2}×2+{(7-7)^2}×4+{(8-7)^2}×2+{(9-7)^2})$
=$\frac{1}{10}×(4+2+0+2+4)=1.2$,
$S_乙^2$=$\frac{1}{10}×({(2-7)^2}+{(4-7)^2}+{(6-7)^2}+{(7-7)^2}×2+{(8-7)^2}×2+{(9-7)^2}×2+{(10-7)^2})$
=$\frac{1}{10}×(25+9+1+0+2+8+9)=5.4$…6分
根据以上的分析与计算填表如下:
| 平均数 | 方差 | 命中9环及9环以上的次数 | |
| 甲 | 7 | 1.2 | 1 |
| 乙 | 7 | 5.4 | 3 |
(Ⅱ)①∵平均数相同,$S_甲^2$<$S_乙^2$,∴甲成绩比乙稳定. …9分
②∵平均数相同,命中9环及9环以上的次数甲比乙少,∴乙成绩比甲好些.…10分
③甲成绩在平均数上下波动;而乙处于上升势头,
从第四次以后就没有比甲少的情况发生,乙较有潜力. …12分.
点评 本题考查平均数、方差、频数的求法及应用,是基础题,考查数据处理能力、运算求解能力,考查转化思想、化归思想.

 阅读快车系列答案
阅读快车系列答案| A. | (-∞,-2]∪[2,+∞) | B. | [0,2] | C. | $[-\sqrt{2},\sqrt{2}]$ | D. | [-2,2] |
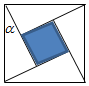 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
| A. | $1-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{4-\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
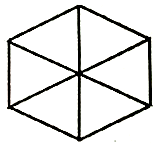 用四种不同的颜色为正六边形(如图)中的六块区域涂色,要求有公共边的区域涂不同颜色,一共有732种不同的涂色方法.
用四种不同的颜色为正六边形(如图)中的六块区域涂色,要求有公共边的区域涂不同颜色,一共有732种不同的涂色方法. 在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.
在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.