题目内容
11．已知集合M={锐角}，N={小于90°的角}，P={第一象限的角}，下列说法：①P⊆N，②N∩P=M，③M⊆P，④（M∪N）⊆P
其中正确的是③．
分析 分别根据角的定义和范围进行判断即可．
解答 解：锐角的范围为0°＜θ＜90°，
小于90°角为θ＜90°包含负角．
第一象限角为k360°＜θ＜k360°+90°，
∴M∪N={小于90°的角}=N，不一定包含于P，
即N∩P=N，M⊆P，
∴其中正确的是：③
故答案为：③．
点评 本题主要考查了交集，并集及其运算，熟练掌握象限角，锐角，以及小于90°的角表示的意义是解本题的关键．是基础题．
练习册系列答案
相关题目
19．将函数f（x）=sin（2x+$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$个单位，所得的图象对应的解析式为（ ）
| A． | y=sin2x | B． | y=cosx | C． | y=sin（2x+$\frac{2π}{3}$） | D． | y=sin（2x-$\frac{π}{6}$） |
16．函数f（x）=sin（x+$\frac{5π}{2}$）的图象关于（ ）
| A． | 原点对称 | B． | y轴对称 | C． | 直线x=$\frac{5π}{2}$对称 | D． | 直线x=-$\frac{5π}{2}$对称 |
20．
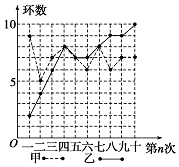甲、乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图所示：
（Ⅰ）请填写表：
（Ⅱ）从下列三个不同的角度对这次测试结果进行分析：
①从平均数和方差相结合看（分析谁的成绩更稳定）；
②从平均数和命中9环及9环以上的次数相结合看（分析谁的成绩好些）；
③从折线图上两人射击命中环数的走势看（分析谁更有潜力）．
甲、乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图所示：（Ⅰ）请填写表：
| 平均数 | 方差 | 命中9环及9环以上的次数 | |
| 甲 | |||
| 乙 |
①从平均数和方差相结合看（分析谁的成绩更稳定）；
②从平均数和命中9环及9环以上的次数相结合看（分析谁的成绩好些）；
③从折线图上两人射击命中环数的走势看（分析谁更有潜力）．
