题目内容
5.设函数f(x)=log2x,在区间(0,5)上随机取一个数x,则f(x)<2的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 解不等式f(x)<2的解,利用几何概型的概率公式即可得到结论.
解答 解:∵log2x,x∈(0,5).
∴由f(x)<2,
得log2x<2
解得0<x<4,
∴根据几何概型的概率公式可得若从区间(0,5)内随机选取一个实数x,
f(x)<2的概率为:$\frac{4-0}{5-0}$=$\frac{4}{5}$,
故选D.
点评 本题主要考查几何概型的概率公式的计算,根据条件求出不等式的解,利用长度比是解决本题的关键.

练习册系列答案
相关题目
16.函数f(x)=sin(x+$\frac{5π}{2}$)的图象关于( )
| A. | 原点对称 | B. | y轴对称 | C. | 直线x=$\frac{5π}{2}$对称 | D. | 直线x=-$\frac{5π}{2}$对称 |
20.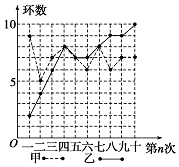 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(Ⅰ)请填写表:
(Ⅱ)从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:(Ⅰ)请填写表:
| 平均数 | 方差 | 命中9环及9环以上的次数 | |
| 甲 | |||
| 乙 |
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
17.设定义在R上的可导函数f(x)的导函数为f′(x),若f(3)=1,且3f(x)+xf′(x)>1,则不等式(x-2017)3f(x-2017)-27>0的解集为( )
| A. | (2014,+∞) | B. | (0,2014) | C. | (0,2020) | D. | (2020,+∞) |
14.以(-1,1)为圆心且与直线x-y=0相切的圆的方程是( )
| A. | (x+1)2+(y-1)2=2 | B. | (x+1)2+(y-1)2=4 | C. | (x-1)2+(y+1)2=1 | D. | (x-1)2+(y+1)2=4 |
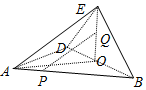 在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.
在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.