设地球半径为R.若甲位于北纬45°东经120°.乙位于北纬45°西经150°.则甲.乙两地的球面距离为$\frac{π}{3}$R．题目和参考答案——青夏教育精英家教网—

题目内容

15．设地球半径为R，若甲位于北纬45°东经120°，乙位于北纬45°西经150°，则甲、乙两地的球面距离为$\frac{π}{3}$R．

分析根据甲、乙两地在同一纬度圈上，计算经度差，求出甲、乙两地对应的AB弦长及球心角，再求球面距离．

解答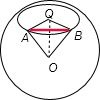解：如图所示，地球表面上甲、乙两地对应的AB的小圆半径是
QA=Rsin45°=$\frac{\sqrt{2}}{2}$R，经度差是90°，
所以AB=$\sqrt{2}$QA=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$R=R；
所以球心角∠AOB=60°=$\frac{π}{3}$，
所以甲、乙两地的球面距离是l=αR=$\frac{π}{3}$R
故答案为：$\frac{π}{3}$R．

点评本题考查了球面距离及其计算问题，也考查了空间想象能力，是基础题．

练习册系列答案

学业测评一卷通小学升学试题汇编系列答案

6．对实数a、b定义运算a⊕b=$\frac{a+b}{1+ab}$，设定义域为R的奇函数f（x），当x∈（0，1）时，f（x）=2^x⊕2^x．
（1）讨论f（x）在π∈（0，1）上的单调性；
（2）求f（x）在（-1，1）上的解析式．

3．已知函数$f（x）={e^{\frac{x}{2}}}$，g（x）=2+lnx，若对任意的实数a，存在实数b∈（0，+∞），使得f（a）=g（b），则b-a的最小值为（　　）

10．设函数f（x）=|x-3|-|x+1|，则关于f（x）的描述正确的是（　　）

	A．	函数f（x）的图象关于直线x=1对称		B．	函数f（x）的图象关于点（1，0）对称
	C．	函数f（x）有最小值，无最大值		D．	函数f（x）在（-∞，-1]上单调递减

20．已知f（x）=$\frac{1}{x}$，则$\underset{lim}{△x→0}$$\frac{f（2+3△x）-f（2）}{△x}$的值是（　　）

7．正项数列{a_n}的前n项和为S_n，满足a_n=2$\sqrt{{S}_{n}}$-1．若对任意的正整数p、q（p≠q），不等式S_P+S_q＞kS_p+q恒成立，则实数k的取值范围为$（-∞，\frac{1}{2}]$．

4．已知p：-x²+8x+20≥0，q：x²-2x+1-m²≤0（m＞0），若p是q充分不必要条件，则实数m的取值范围是m≥9．

5．圆x²+y²=4与圆（x-3）²+y²=1的位置关系为（　　）