题目内容
已知函数f(x)=2ax2+2x-3,如果函数y=f(x)在区间[-1,1]上有零点,则实数a的取值范围为 .
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:讨论a以确定函数f(x)是一次函数还是二次函数及二次函数的开口方向及对称轴,再由函数的零点的判定定理确定a的取值范围.
解答:
解:当a=0时,f(x)=2x-3在区间[-1,1]上没有零点;
当a>0时,f(0)=-3<0,
故f(-1)=2a-5≥0或f(1)=2a+2-3≥0;
解得,a≥
;
当0<-
≤1,即a≤-
时,
f(-
)=-
-3<0,故不成立;
当-
>1,即-
<a<0时,
f(1)=2a+2-3≥0,a≥
;
综上所述,a≥
;
故答案为:a≥
.
当a>0时,f(0)=-3<0,
故f(-1)=2a-5≥0或f(1)=2a+2-3≥0;
解得,a≥
| 1 |
| 2 |
当0<-
| 1 |
| 2a |
| 1 |
| 2 |
f(-
| 1 |
| 2a |
| 1 |
| 2a |
当-
| 1 |
| 2a |
| 1 |
| 2 |
f(1)=2a+2-3≥0,a≥
| 1 |
| 2 |
综上所述,a≥
| 1 |
| 2 |
故答案为:a≥
| 1 |
| 2 |
点评:本题考查了二次函数的性质及函数零点的判定定理的应用,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知命题P:复数z=1-i在复平面内对应的点位于第四象限;命题q:?x0>0,使x0=cosx0,则下列命题中为真命题的是( )
| A、(¬p)∧(¬q) |
| B、(¬p)∧q |
| C、p∧(¬q) |
| D、p∧q |
已知四棱锥S-ABCD的所有棱长都相等,E是SB的中点,则AE,SD所成的角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=cos2x-2
sinxcosx下列命题中正确的是( )
(1)若存在x1,x2有x1-x2=z时,f(x1)=f(x2)成立
(2)f(x)在[-
,
]是单调递增
(3)函数f(x)关于点(
,0)成中心对称图象
(4)将函数f(x)的图象向左平移
个单位后将与y=2sin2x重合.
| 3 |
(1)若存在x1,x2有x1-x2=z时,f(x1)=f(x2)成立
(2)f(x)在[-
| π |
| 6 |
| π |
| 3 |
(3)函数f(x)关于点(
| π |
| 12 |
(4)将函数f(x)的图象向左平移
| 5π |
| 12 |
| A、(1)(2) |
| B、( 1)(3) |
| C、( 1)(2)(3) |
| D、(1)(3)(4) |
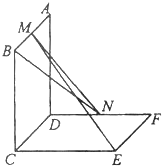 如图,已知两个正方形ABCD 和DCEF不在同一平面内,且平面ABCD⊥平面DCEF,M,N分别为AB,DF的中点.
如图,已知两个正方形ABCD 和DCEF不在同一平面内,且平面ABCD⊥平面DCEF,M,N分别为AB,DF的中点. 在正方体ABCD-A1B1C1D1中,P,Q分别是AB,B1C1上的点AP=B1Q,N是PQ的中点,M是正方形ABB1A1的中心.求证:
在正方体ABCD-A1B1C1D1中,P,Q分别是AB,B1C1上的点AP=B1Q,N是PQ的中点,M是正方形ABB1A1的中心.求证: