题目内容
直线y=x-1被椭圆
+y2=1截得的弦长为 .
| x2 |
| 4 |
考点:直线与圆锥曲线的关系
专题:计算题,圆锥曲线中的最值与范围问题
分析:由题意联立方程
,设直线y=x-1被椭圆
+y2=1的交点为(m,m-1)(n,n-1),从而化简可得|m-n|=
;从而求弦长.
|
| x2 |
| 4 |
| 8 |
| 5 |
解答:
解:由题意,
,
消去y整理得,
x(5x-8)=0;
设直线y=x-1被椭圆
+y2=1的交点为(m,m-1)(n,n-1);
故|m-n|=
;
故直线y=x-1被椭圆
+y2=1截得的弦长为
;
故答案为:
.
|
消去y整理得,
x(5x-8)=0;
设直线y=x-1被椭圆
| x2 |
| 4 |
故|m-n|=
| 8 |
| 5 |
故直线y=x-1被椭圆
| x2 |
| 4 |
| 8 |
| 5 |
| 2 |
故答案为:
| 8 |
| 5 |
| 2 |
点评:本题考查了直线与圆锥曲线的位置关系的应用,同时考查了弦长的求法,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
函数y=-sinx(x∈R)的单调增区间为( )
A、[-
| ||||
B、[
| ||||
| C、[2kπ,π+2kπ](k∈Z) | ||||
| D、[-π+2kπ,2kπ](k∈Z) |
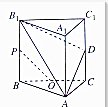 如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:
如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证: 已知三视图如图所示,画出原几何体.
已知三视图如图所示,画出原几何体.