题目内容
分别在区间[1,5]、[1,4]内各任取一个实数依次为m,n,则m>n的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意知本题是一个几何概型,根据所给的条件作出试验发生是包含的所有事件是一个矩形区域,做出面积,看出满足条件的事件对应的面积,根据几何概型公式得到结果.
解答:
解:所求概率为由约束条件
确定的区域的面积与由不等式
确定的平面区域的面积的比值,
其值为1-
=
.
故选:C
|
|
其值为1-
| ||
| 12 |
| 5 |
| 8 |
故选:C
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
已知函数f(x)=
则方程f(x)-a=0有四个实根的充要条件为( )
|
| A、a≥1 | B、a≤3 |
| C、1≤a≤3 | D、1<a<3 |
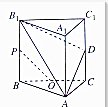 如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:
如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证: 如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.