题目内容
已知定义域为R的函数f(x)=
是奇函数.
(1)求a、b的值;
(2)用定义证明:函数f(x)在R上是减函数;
(3)已知不等式f(logm
)+f(-1)>0恒成立,求实数m的取值范围.
| -2x+b |
| 2x+1+a |
(1)求a、b的值;
(2)用定义证明:函数f(x)在R上是减函数;
(3)已知不等式f(logm
| 3 |
| 4 |
考点:函数恒成立问题,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)由题意可得f(-x)+f(x)=0恒成立,故可得a=2,b=1或a=-2,b=-1,注意检验;
(2)由(1)可求得f(x)=
,利用定义证明即可;
(3)借助函数的性质化不等式f(logm
)+f(-1)>0为logm
<1,从而解得.
(2)由(1)可求得f(x)=
| 1 |
| 2 |
| 1-2x |
| 2x+1 |
(3)借助函数的性质化不等式f(logm
| 3 |
| 4 |
| 3 |
| 4 |
解答:
解:(1)由题意,
f(-x)+f(x)=
+
=0,
即(2-x+1+a)(-2x+b)+(-2-x+b)(2x+1+a)=0;
整理可得,
-2+2b2-x-a2x+ab-2+2b2x-a2-x+ab=0;
故
,
解得,a=2,b=1或a=-2,b=-1;
当a=-2,b=-1时,定义域不是R,故不成立;
故a=2,b=1;
(2)证明:由(1)知,f(x)=
;
任取x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=
•
-
•
=
,
∵x1<x2,
∴0<2x1<2x2;
∴f(x1)-f(x2)>0;
故函数f(x)在R上是减函数;
(3)∵f(x)=
是R上的奇函数,
∴f(logm
)+f(-1)>0可化为f(logm
)>f(1);
又∵函数f(x)在R上是减函数;
故logm
<1;
①当m>1时,成立;
②当0<m<1时,
>m;
故0<m<
;
综上所述,m>1或0<m<
.
f(-x)+f(x)=
| -2-x+b |
| 2-x+1+a |
| -2x+b |
| 2x+1+a |
即(2-x+1+a)(-2x+b)+(-2-x+b)(2x+1+a)=0;
整理可得,
-2+2b2-x-a2x+ab-2+2b2x-a2-x+ab=0;
故
|
解得,a=2,b=1或a=-2,b=-1;
当a=-2,b=-1时,定义域不是R,故不成立;
故a=2,b=1;
(2)证明:由(1)知,f(x)=
| 1 |
| 2 |
| 1-2x |
| 2x+1 |
任取x1,x2∈R,且x1<x2,
则f(x1)-f(x2)=
| 1 |
| 2 |
| 1-2x1 |
| 2x1+1 |
| 1 |
| 2 |
| 1-2x2 |
| 2x2+1 |
=
| 2x2-2x1 |
| (2x1+1)(2x2+1) |
∵x1<x2,
∴0<2x1<2x2;
∴f(x1)-f(x2)>0;
故函数f(x)在R上是减函数;
(3)∵f(x)=
| 1 |
| 2 |
| 1-2x |
| 2x+1 |
∴f(logm
| 3 |
| 4 |
| 3 |
| 4 |
又∵函数f(x)在R上是减函数;
故logm
| 3 |
| 4 |
①当m>1时,成立;
②当0<m<1时,
| 3 |
| 4 |
故0<m<
| 3 |
| 4 |
综上所述,m>1或0<m<
| 3 |
| 4 |
点评:本题考查了函数的性质的判断与证明,同时考查了恒成立问题,属于中档题.

练习册系列答案
相关题目
若集合M={y|x2=y,x∈R},集合N={y|x+y=0,x∈R},则M∩N等于( )
| A、{y|y∈R} |
| B、{(-1,1),(0,0)} |
| C、{(0,0)} |
| D、{x|x≥0} |
已知函数f(x)=
则方程f(x)-a=0有四个实根的充要条件为( )
|
| A、a≥1 | B、a≤3 |
| C、1≤a≤3 | D、1<a<3 |
把函数y=sin(2x+
)的图象向右平移
个单位,所得的图象对应的函数是( )
| π |
| 4 |
| π |
| 4 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
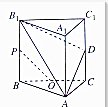 如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证:
如图所示,ABC-A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点,P是B1B的中点,O是△ABC的中心,求证: 已知三视图如图所示,画出原几何体.
已知三视图如图所示,画出原几何体. 如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.