题目内容
9.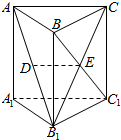 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:(Ⅰ)DE∥平面AA1C1C;
(Ⅱ)BC1⊥AB1.
分析 (1)由三角形中位线定理得DE∥AC,由此能证明DE∥平面AA1C1C.
(2)推导出BC1⊥B1C,AC⊥CC1,AC⊥BC,从而AC⊥平面BCC1B1,进而AC⊥BC1,由此能证明BC1⊥AB1.
解答 证明:(1)∵在直三棱柱ABC-A1B1C1中,BC1∩B1C=E,
∴E是B1C的中点,
∵AB1的中点为D,∴DE∥AC,
∵AC?平面AA1C1C,DE?平面AA1C1C,
∴DE∥平面AA1C1C.
(2)∵在直三棱柱ABC-A1B1C1中,BC=CC1,
∴BC1⊥B1C,AC⊥CC1,又AC⊥BC,BC∩CC1=C,
∴AC⊥平面BCC1B1,∴AC⊥BC1,
∵AC∩B1C=C,∴BC1⊥平面ACB1,
∴BC1⊥AB1.
点评 本题考查线面平行的证明,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
4.在四边形ABCD中,若$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(3,-4),$\overrightarrow{CD}$=(-2,-3),则四边形ABCD的面积是( )
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
18.在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |