题目内容
3．光线通过一块玻璃板，其强度将会失掉10%，先将6块玻璃板叠加制成玻璃墙，求光线通过该玻璃板后的强度为通过一块玻璃板后强度的百分率（精确到0.1）？分析 分别求出光线通过6块玻璃后强度和光线通过通过一块玻璃板后强度，再求光线通过该玻璃板后的强度为通过一块玻璃板后强度的百分率．
解答 解：光线通过一块玻璃，其强度要损失10%，把6块这样的玻璃重叠起来，
设光线原来的强度为a，通过6块玻璃后强度为y．
则y=a（1-10%）6≈0.5314a，
∵光线通过通过一块玻璃板后强度为a（1-10%）=0.9a，
∴光线通过该玻璃板后的强度为通过一块玻璃板后强度的百分率为：
$\frac{0.5314a}{0.9a}$≈59.04%．
点评 本题考查函数性质在生产生活中的应用，是基础题，解题时要注意函数性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
4．函数f（x）是定义域在R上的偶函数，且f（x）=-f（2-x），若f（x）在区间[1，2]上是减函数，则f（x）（ ）
| A． | 在区间[-2，-1]上是增函数，在区间[3，4]上是增函数 | |
| B． | 在区间[-2，-1]上是增函数，在区间[3，4]上是减函数 | |
| C． | 在区间[-2，-1]上是减函数，在区间[3，4]上是增函数 | |
| D． | 在区间[-2，-1]上是减函数，在区间[3，4]上是减函数 |
8．在△ABC中，角A，B，C的对应边分别为a，b，c，若${a^2}+{b^2}-{c^2}=\sqrt{3}ab$，则角C的值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{6}$或$\frac{5π}{6}$ | D． | $\frac{π}{3}$或$\frac{2π}{3}$ |
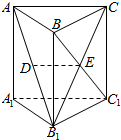如图，在直三棱柱ABC-A1B1C1中，已知AC⊥BC，BC=CC1，设AB1的中点为D，BC1∩B1C=E．求证：