题目内容
4．在四边形ABCD中，若$\overrightarrow{AB}$=（6，1），$\overrightarrow{BC}$=（3，-4），$\overrightarrow{CD}$=（-2，-3），则四边形ABCD的面积是（ ）| A． | 20 | B． | 30 | C． | 40 | D． | 50 |
分析 根据向量的坐标分别求出四个点的坐标，并画出坐标系，间接求面积．
解答 
解：设A（0，0），则B（6，1），C（9，-3），D（7，-6），如图
四边形ABCD的面积是大正方形FGHI的面积减去四个直角三角形的面积，
所以四边形ABCD的面积是7×9-$\frac{1}{2}$×（1×6+3×4+2×3+7×6）=30；
故选：B．
点评 本题考查了数形结合、间接法求四边形面积；关键是正确画图，直观分析．
练习册系列答案
相关题目
19．已知$\overrightarrow{p}$=（a，b），$\overrightarrow{q}$=（c，d），规定向量$\overrightarrow{p}$，$\overrightarrow{q}$之间的一个运算符号“*”，$\overrightarrow{p}$*$\overrightarrow{q}$=（ac-bd，ad+bc），若$\overrightarrow{p}$=（0，1），$\overrightarrow{p}$*$\overrightarrow{q}$=（-4，-3），则$\overrightarrow{q}$等于（ ）
| A． | （3，-4） | B． | （3，4） | C． | （-3，4） | D． | （-3，-4） |
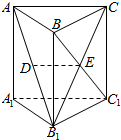如图，在直三棱柱ABC-A1B1C1中，已知AC⊥BC，BC=CC1，设AB1的中点为D，BC1∩B1C=E．求证：