题目内容
18.在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
分析 根据导函数判断函数f(x)=ex+4x-3单调递增,运用零点判定定理,判定区间.
解答 解:∵函数f(x)=ex+4x-3
∴f′(x)=ex+4
当x>0时,f′(x)=ex+4>0
∴函数f(x)=ex+4x-3在(-∞,+∞)上为f(0)=e0-3=-2<0,
f(1)=e+4-3>0,
∴f(0)•f(1)<0,
∴函数f(x)=ex+4x-3的零点所在的区间为(0,1)
故选:C.
点评 本题考察了函数零点的判断方法,借助导数,函数值,属于中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
8.在△ABC中,角A,B,C的对应边分别为a,b,c,若${a^2}+{b^2}-{c^2}=\sqrt{3}ab$,则角C的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
8.麦当劳店每天的房租、人员工资等固定成本为200元,某种食品每份的成本价是5元,销售单价与日均销售量的关系如下表所示:
请你根据以上数据作出分析,该麦当劳店怎样定价才能获得最大利润?
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/份 | 440 | 400 | 360 | 320 | 280 | 240 | 200 |
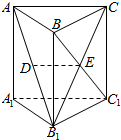 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证: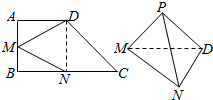 在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.
在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.