题目内容

11．若曲线f（x）=x（x-m）2在x=1处取得极小值，则m的值是1．

分析 通过对函数f（x）求导，根据函数在x=1处有极值，可知f'（1）=0，解得m的值，再验证可得结论．

解答 解：求导函数可得f'（x）=3x2-4mx+m2，
∴f'（1）=3-4m+m2=0，解得m=1，或m=3，
当m=1时，f'（x）=3x2-4x+1=（3x-1）（x-1），函数在x=1处取到极小值，符合题意；
当m=3时，f'（x）=3x2-12x+9=3（x-1）（x-3），函数在x=1处取得极大值，不符合题意，
∴m=1，
故答案为：1．

点评 本题考查了函数的极值问题，考查学生的计算能力，正确理解极值是关键．

练习册系列答案
相关题目
1．用数学归纳法证明（x+1）n+1+（x+2）2n-1（n∈N*）能被x2+3x+3 整除．
2．已知sin（π+α）=-$\frac{1}{2}$，求tan（$\frac{π}{2}$-α）的值．
19．已知甲、乙、丙等6人．
（1）这6人同时参加一项活动，必须有人去，去几人自行决定，共有多少种不同的去法？
（2）这6人同时参加6项不同的活动，每项活动限1人参加，求甲不参加第一项活动且乙不参加第三项活动的概率．
（3）这6人同时参加4项不同的活动，求每项活动至少有1人参加的概率．
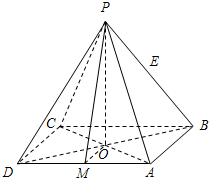6．如图所示，四棱锥P-ABCD中，PA=PB=PC=PD，AB=a，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$．
（1）求侧面PAD与底面ABCD所成的二面角的大小；
（2）若E是PB的中点，求异面直线PD与AE所成角的正切值．
16．已知半径为5的圆的圆心在x轴上，圆心的横坐标是整数，且圆与直线4x+3y-29=0相切，设直线ax-y+5=0（a
＞0）与圆相交于A，B两点．
（1）求圆的标准方程；
（2）求实数a的取值范围；
（3）是否存在实数a，使得线AB的垂直平分线l过点P（-2，4）？
3．如图，已知四边形ABCD为菱形，且∠A=60°，E，F分别为AB，AD的中点，现将四边形EBCD沿DE折起至EBHD．

（Ⅰ）求证：EF∥平面ABH；
（Ⅱ）若平面EBHD⊥平面ADE，求二面角B-AH-D的平面角的余弦值．
20．已知函数f（x）=x2e-x，则f（x）的极大值为$\frac{4}{{e}^{2}}$．
1．已知长方体ABCD-A1B1C1D1的所有顶点都在球O的球面上，AB=AD=1，AA1=2，则球O的球面面积为（　　）
A．2πB．4πC．6πD．24π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网