题目内容
2.函数f(x)=($\frac{1}{2}$)${\;}^{{x}^{2}-4x+3}$(1)求函数f(x)的单调区间和值域;
(2)若满足x∈[0,3],求函数f(x)的最大值和最小值.
分析 (1)令t=x2-4x+3,则y=($\frac{1}{2}$)t在R上递减,运用复合函数的单调性:同增异减,求得二次函数的区间,即可得到所求单调区间和值域;
(2)由(1)的单调性可得f(x)在[0,2]上单调递增,在[2,3]上单调递减,即有f(2)取得最大值,比较f(0)和f(3),可知最小值.
解答 解:(1)令t=x2-4x+3,
则y=($\frac{1}{2}$)t在R上递减,
由t在(-∞,2)递减,(2,+∞)递增,
可得函数f(x)的单调递增区间为(-∞,2),
单调递减区间为为(2,+∞),
当x=2时,函数数f(x)有最大值,
f(2)=2,且f(x)=($\frac{1}{2}$)${\;}^{{x}^{2}-4x+3}$>0,
故值域为(0,2];
(2)由(1)知,函数f(x)在[0,2]上单调递增,在[2,3]上单调递减,
所以最大值为f(2)=2,
由f(0)=$\frac{1}{8}$,f(3)=1,所以最小值为$\frac{1}{8}$.
点评 本题考查复合函数的单调区间和最值、值域的求法,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
13.原点到直线y=-$\frac{1}{2}$x+$\frac{5}{2}$的距离为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
10.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知△ABC的面积为3$\sqrt{15}$,b-c=2,cos A=-$\frac{1}{4}$,则a的值为( )
| A. | 4 | B. | 2 | C. | $\sqrt{3}$ | D. | 8 |
11.复数Z=$\frac{-2i}{1+2i}$(i为虚数单位)所对应复平面内的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
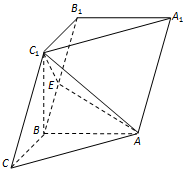 如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=BC1=$\sqrt{2}$,AB=CC1=2,点E在棱BB1上.
如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=BC1=$\sqrt{2}$,AB=CC1=2,点E在棱BB1上.