题目内容
10．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知△ABC的面积为3$\sqrt{15}$，b-c=2，cos A=-$\frac{1}{4}$，则a的值为（ ）| A． | 4 | B． | 2 | C． | $\sqrt{3}$ | D． | 8 |
分析 cos A=-$\frac{1}{4}$，可得sinA=$\sqrt{1-co{s}^{2}A}$．由$\frac{1}{2}$bcsinA=$\frac{1}{2}bc×\frac{\sqrt{15}}{4}$=$3\sqrt{15}$，b-c=2，解得b，c．再利用余弦定理即可得出．
解答 解：∵cos A=-$\frac{1}{4}$，∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{15}}{4}$．
∵$\frac{1}{2}$bcsinA=$\frac{1}{2}bc×\frac{\sqrt{15}}{4}$=$3\sqrt{15}$，b-c=2，解得b=6，c=4．
∴a2=b2+c2-2bccos A=62+42-2×$6×4×（-\frac{1}{4}）$=64，
解得a=8．
故选：D．
点评 本题考查了三角形面积计算公式、余弦定理、同角三角函数基本关系式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
20．
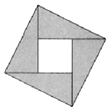如图，阴影部分是由四个全等的直角三角形组成的图形，在大正方形内随机取一点，这一点落在小正方形内的概率为 $\frac{1}{5}$，若直角三角形的两条直角边的长分别为a，b（a＞b），则$\frac{b}{a}$=（ ）
如图，阴影部分是由四个全等的直角三角形组成的图形，在大正方形内随机取一点，这一点落在小正方形内的概率为 $\frac{1}{5}$，若直角三角形的两条直角边的长分别为a，b（a＞b），则$\frac{b}{a}$=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
如图，四边形ABCD为矩形，EA⊥平面ABCD，EF∥AB，AB=2AE=2EF=4．
15．已知全集U={x|x≤5}，集合A={x|-3＜x＜4}，B={x|-5≤x≤3}，则（∁UA）∩B=（ ）
| A． | {x|-5≤x≤-3} | B． | {x|4＜x＜5，或x≤-3} | C． | {x|-5＜x＜-3} | D． | {x|-5＜x＜5} |