题目内容
19.某班4名学生的数学和物理成绩如表:| 学生 学科 | A | B | C | D |
| 数学成绩(x) | 86 | 73 | 69 | 63 |
| 物理成绩(y) | 76 | 71 | 64 | 59 |
(2)一名学生的数学成绩是90分,试预测他的物理成绩.
附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})•({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 (1)计算$\overline{x}$、$\overline{y}$,求出回归系数,写出回归方程;
(2)计算x=90时$\stackrel{∧}{y}$的值即可.
解答 解:(1)计算$\overline{x}$=$\frac{1}{4}$×(86+73+69+63)=72.75,
$\overline{y}$=$\frac{1}{4}$×(76+71+64+59)=67.5,
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})•({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{(86-72.75)(76-67.5)+…+(63-72.75)(59-67.5)}{{(86-72.75)}^{2}{+…+(63-72.75)}^{2}}$≈0.74,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=67.5-0.74×72.75=13.7,
∴y对x的线性回归方程$\stackrel{∧}{y}$=0.74x+13.7;
(2)x=90时,$\stackrel{∧}{y}$=0.74×90+13.7=80.3,
即一名学生的数学成绩是90分时,预测他的物理成绩为80.3分.
点评 本题考查了线性回归方程的计算问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知集合A={x|x2-4x-5>0},B={x|x>2},则集合A∩B=( )
| A. | ∅ | B. | (-∞,1) | C. | (2,+∞) | D. | (5,+∞) |
4.近来景德镇市棚户区改造进行的如火如荼,加上城市人居环境的不断改善,我市房地产住宅销售价格节节攀升,一部分刚需住户带来了不小的烦恼,下表为我市2017.1-2017.5这5月住宅价格与月份的关系.
(1)通过计算线性相关系数判断住宅价y千元/平米与月份x的线性相关程度(精确到0.01)
(2)用最小二乘法得到的线性回归直线去近似拟合x,y的关系.
①求y关于x的回归方程;②试估计按照这个趋势下去,将在不久的哪个年月份,房价将突破万元/平米的大关.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 住宅价格y 千元/平米 | 4.8 | 5.4 | 6.2 | 6.6 | 7 |
(2)用最小二乘法得到的线性回归直线去近似拟合x,y的关系.
①求y关于x的回归方程;②试估计按照这个趋势下去,将在不久的哪个年月份,房价将突破万元/平米的大关.
9.设a=log38,b=21.2,c=0.33.1,则( )
| A. | b<a<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
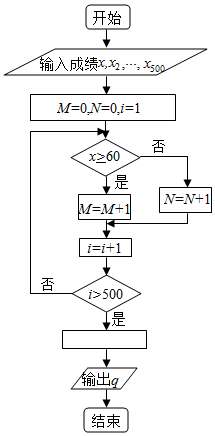 如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入$q=\frac{M}{M+N}$.
如图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入$q=\frac{M}{M+N}$.