题目内容
14.抛物线x=4y2的焦点坐标是 ( )| A. | ($\frac{1}{16}$,0) | B. | (1,0) | C. | (0,$\frac{1}{16}$) | D. | (0,1 ) |
分析 化简抛物线方程为标准方程,然后求解即可.
解答 解:抛物线x=4y2的标准方程为:y2=$\frac{1}{4}$x它的焦点坐标是($\frac{1}{16}$,0).
故选:A.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
2.已知不等式$\frac{{{2^x}+1}}{3}>1-\frac{{{2^x}-1}}{2}$的解集为M,则下列说法正确的是( )
| A. | {0}⊆M | B. | M=∅ | C. | -1∈M | D. | 2∈M |
6.函数$y=\sqrt{{{log}_2}(x-3)}$的定义域是( )
| A. | (3,+∞) | B. | (3,4] | C. | (4,+∞) | D. | [4,+∞) |
3.设F1,F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{25}=1(a<5)$的两个焦点,且|F1F2|=8,弦AB过点F2,则△ABF1的周长为( )
| A. | 12 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
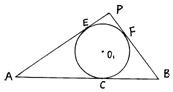 如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.
如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.