题目内容
函数f(x)的导函数f′(x)的图象如图,则y=f(x)的图象最有可能是( )
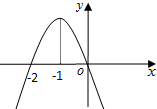
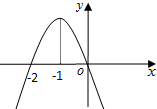
A、 |
B、 |
C、 |
D、 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:直接根据导函数在x∈(-2,0)上的符号得到原函数在x∈(-2,0)上的单调性,由此可得结论.
解答:
解:因为函数y=f(x)的导函数在x∈(-2,0)时恒大于0,所以原函数y=f(x)的图象在x∈(-2,0)时为增函数.
选项中只有B符合.
故选B
选项中只有B符合.
故选B
点评:本题主要考查函数的单调性与其导函数的正负之间的关系.属基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
函数f(x)的图象如图所示,下列数值排序正确的是( )
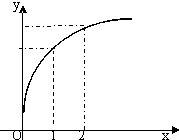

| A、0<f′(1)<f′(2)<f(2)-f(1) |
| B、0<f′(2)<f(2)-f(1)<f′(1) |
| C、0<f′(2)<f′(1)<f(2)-f(1) |
| D、0<f(2)-f(1)<f′(1)<f′(2) |
关于x的方程x2+(m-2)x+5-m=0的两根均大于2,则实数m的取值范围是( )
| A、(-5,-4] |
| B、(-∞,-5)∪(-5,-4) |
| C、(-∞,-4] |
| D、(-∞,-2) |
已知函数f(x)=sinx+cosx,则函数f(x)的一个单调递增区间为( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
在平行四边形ABCD中,
+
+
=( )
| AB |
| CA |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
对于实数a和b,定义运算“*”:
,设f(x)=(2x-1)*(x-1),且关于x的方程f(x)=a(a∈R)恰有三个互不相等的实数根,则实数a的取值范围
是( )
|
是( )
A、(0,
| ||
B、[0,
| ||
C、[0,
| ||
D、(0,
|
已知数列{an}满足a1=4,an=4-
(n≥2),则a6=( )
| 4 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在(1+x)n的二项展开式中,若只有x5的项的系数最大,则n的值为( )
| A、5 | B、6 | C、20 | D、10 |
