题目内容
12.已知平面直角坐标系xoy,以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的参数方程为$\left\{\begin{array}{l}x=2cosφ\\ y=2+2sinφ\end{array}\right.(φ为参数)$.点A,B是曲线C上两点,点A,B的极坐标分别为$({ρ_1},\frac{π}{3}),({ρ_2},\frac{5π}{6})$.则|AB|=( )| A. | 4 | B. | $\sqrt{7}$ | C. | $4\sqrt{7}$ | D. | 5 |
分析 求出A,B的坐标,利用两点间的距离公式,即可得出结论.
解答 解:曲线C的参数方程为$\left\{\begin{array}{l}x=2cosφ\\ y=2+2sinφ\end{array}\right.(φ为参数)$.
普通方程为x2+(y-2)2=4.极坐标方程为ρ=4sinθ,
θ=$\frac{π}{3}$,ρ1=2$\sqrt{3}$,∴A($\sqrt{3}$,3),
θ=$\frac{5π}{6}$,ρ2=2,∴B(-$\sqrt{3}$,1),
∴|AB|=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4,
故选A.
点评 本题考查三种方程的转化,考查两点间的距离公式,比较基础.

练习册系列答案
相关题目
3.已知复数$z=\frac{5}{2-i}$(i是复数单位),则复数z为( )
| A. | 2+i | B. | -2+i | C. | -2-i | D. | 2-i |
20.已知球的直径SC=4,A、B 是该球面上的两点且AB=2$\sqrt{2}$,∠ASC=30°,∠SCB=45°,则三棱锥S-ABC的体积为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
17.下列哪个命题的逆命题为真命题的是( )
| A. | 若a>b,则ac>bc | B. | 若a2>b2,则a>b>0 | ||
| C. | 若|x-3|>1,则2<x<4 | D. | 若|x2-3|>1,则$\sqrt{2}<x<2$ |
4.有一段“三段论”,其推理是这样的:
对于可导函数f(x),若f′(x0)=0,则x=x0是函数f(x)的极值点…大前提因为函数f(x)=x3满足f′(0)=0,…小前提所以x=0是函数f(x)=x3的极值点”,结论以上推理( )
对于可导函数f(x),若f′(x0)=0,则x=x0是函数f(x)的极值点…大前提因为函数f(x)=x3满足f′(0)=0,…小前提所以x=0是函数f(x)=x3的极值点”,结论以上推理( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 没有错误 |
2.方程$|sin\frac{π}{2}x|=lg|x|$有多少个根?( )
| A. | 9 | B. | 10 | C. | 18 | D. | 20 |
 如图椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左顶点A的距离为4+2$\sqrt{2}$.
如图椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左顶点A的距离为4+2$\sqrt{2}$.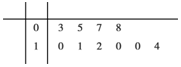 学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下:
学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下: