题目内容
在Rt△ABC中,AB=5,BC=4,∠ACB=90°,若使其绕直线BC旋转一周,则其形成的几何体的体积是 .
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:Rt△ABC绕直线BC旋转一周,形成的几何体以以AC为半径,以BC为高的圆锥,求出圆锥的底面半径,代入圆锥体积公式,可得答案.
解答:
解:Rt△ABC绕直线BC旋转一周,
形成的几何体以以AC为半径,以BC为高的圆锥,
∵AB=5,BC=4,∠ACB=90°,
∴AC=3,
故几何体的体积V=
π•AC2•BC=12π,
故答案为:12π
形成的几何体以以AC为半径,以BC为高的圆锥,
∵AB=5,BC=4,∠ACB=90°,
∴AC=3,
故几何体的体积V=
| 1 |
| 3 |
故答案为:12π
点评:本题考查的知识点是旋转体,其中根据已知分析出形成的几何体以以AC为半径,以BC为高的圆锥,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f′(x)是 f(x)的导函数,则
=( )
| lim |
| t→0 |
| f(3)-f(3-t) |
| t |
| A、f′(3) |
| B、f′(t) |
| C、-f′(3) |
| D、-f′(t) |
 在三棱锥S-ABC中,O是AB的中点,SA=SB=
在三棱锥S-ABC中,O是AB的中点,SA=SB=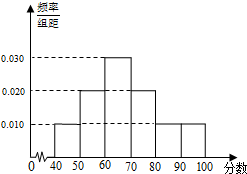 某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是
某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是