题目内容
 在三棱锥S-ABC中,O是AB的中点,SA=SB=
在三棱锥S-ABC中,O是AB的中点,SA=SB=| 2 |
(1)求证:平面SOC⊥平面ABC;
(2)求二面角O-SC-A的平面角的正切值.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间角
分析:(1)由已知条件推导出SO⊥AB,CO⊥AB,从而得到AB⊥平面SOC,由此能证明平面SOC⊥平面ABC.
(2)取SC中点D,连结OD、AD,由已知条件推导出∠ADO是二面角二面角O-SC-A的平面角,由此能求出二面角O-SC-A的平面角的正切值.
(2)取SC中点D,连结OD、AD,由已知条件推导出∠ADO是二面角二面角O-SC-A的平面角,由此能求出二面角O-SC-A的平面角的正切值.
解答:
(1)证明:在三棱锥S-ABC中,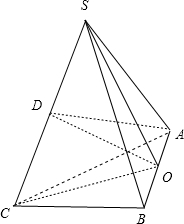
∵O是AB的中点,SA=SB=
,其余棱长均为2,
∴SO⊥AB,CO⊥AB,SO∩CO=O,
∴AB⊥平面SOC,
∵AB?平面ABC,
∴平面SOC⊥平面ABC.
(2)解:取SC中点D,连结OD、AD,
由题意知SO=CO=
,SA=CA=2,
∴OD⊥SC,AD⊥SC,
∴∠ADO是二面角二面角O-SC-A的平面角,
由题意知OD=
=
,AD=
=
,AO=1,
∴cos∠ADO=
=
,
∴sin∠ADO=
=
,
∴tan∠ADO=
=
.
∴二面角O-SC-A的平面角的正切值为
.

∵O是AB的中点,SA=SB=
| 2 |
∴SO⊥AB,CO⊥AB,SO∩CO=O,
∴AB⊥平面SOC,
∵AB?平面ABC,
∴平面SOC⊥平面ABC.
(2)解:取SC中点D,连结OD、AD,
由题意知SO=CO=
| 3 |
∴OD⊥SC,AD⊥SC,
∴∠ADO是二面角二面角O-SC-A的平面角,
由题意知OD=
| 3-1 |
| 2 |
| 4-1 |
| 3 |
∴cos∠ADO=
| 3+2-1 | ||||
2
|
| ||
| 3 |
∴sin∠ADO=
1-(
|
| ||
| 3 |
∴tan∠ADO=
| ||||
|
| ||
| 2 |
∴二面角O-SC-A的平面角的正切值为
| ||
| 2 |
点评:本题考查平面与平面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
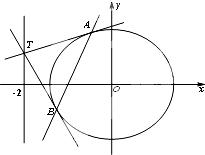 设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q.动点M满足
设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q.动点M满足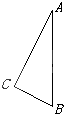 已知直角三角形ABC的斜边长AB=2,现以斜边AB为轴旋转一周,得旋转体.
已知直角三角形ABC的斜边长AB=2,现以斜边AB为轴旋转一周,得旋转体.