题目内容
5.已知圆C:(x-1)2+y2=4(1)求过点P(3,3)且与圆C相切的直线l的方程;
(2)已知直线m:x-y+1=0与圆C交于A、B两点,求|AB|
分析 (1)设出切线方程,求出圆的圆心与半径,利用圆心到直线的距离等于半径,求出k,写出切线方程即可;
(2)求出圆心到直线的距离,利用勾股定理求弦|AB|的长.
解答 解:(1)设切线方程为y-3=k(x-3),即kx-y-3k+3=0,
∵圆心(1,0)到切线l的距离等于半径2,
∴$\frac{|-2k+3|}{\sqrt{{k}^{2}+1}}$=2,解得k=$\frac{5}{12}$,
∴切线方程为y-3=$\frac{5}{12}$(x-3),即5x-12y+21=0,
当过点M的直线的斜率不存在时,其方程为x=3,圆心(1,0)到此直线的距离等于半径2,
故直线x=3也适合题意.
所以,所求的直线l的方程是5x-12y+21=0或x=3.
(2)圆心到直线的距离d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴|AB|=2$\sqrt{4-2}$=2$\sqrt{2}$.
点评 本题考查直线与圆的位置关系,考查圆的切线方程的求法,注意直线的斜率存在与不存在情况,是本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
16.函数$f(x)=\left\{\begin{array}{l}2x-{x^2},0≤x≤3\\{x^2}+6x,-2≤x<0\end{array}\right.$的值域是( )
| A. | [-8,1] | B. | [-8,-3] | C. | R | D. | [-9,1] |
13.直线l:x+y+1=0的倾斜角为( )
| A. | 45° | B. | 135° | C. | 1 | D. | -1 |
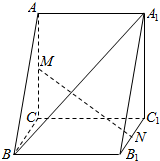 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.