题目内容
若不等式-2≤x2-2ax+a≤-1有唯一解,则a的取值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:二次函数的性质,根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:结合二次函数的性质知,不等式-2≤x2-2ax+a≤-1有唯一解可化为x2-2ax+a=-1有唯一解,从而解得.
解答:
解:∵不等式-2≤x2-2ax+a≤-1有唯一解,
∴x2-2ax+a=-1有唯一解,
即△=(-2a)2-4(a+1)=0;
即a2-a-1=0;
解得,a=
;
故选D.
∴x2-2ax+a=-1有唯一解,
即△=(-2a)2-4(a+1)=0;
即a2-a-1=0;
解得,a=
1±
| ||
| 2 |
故选D.
点评:本题考查了二次函数与二次不等式的关系应用,属于基础题.

练习册系列答案
相关题目
若x,y满足不等式组
,且y+
x的最大值为2,则实数m的值为( )
|
| 1 |
| 2 |
| A、-2 | ||
B、-
| ||
| C、1 | ||
D、
|
过空间两点作直线l的垂面( )
| A、能作一个 |
| B、最多只能作一个 |
| C、可作多个 |
| D、以上都不对 |
如图在棱长均为2的正四棱锥P-ABCD中,点E为PC中点,则下列命题正确的是( )


A、BE平行面PAD,且直线BE到面PAD距离为
| ||||
B、BE平行面PAD,且直线BE到面PAD距离为
| ||||
C、BE不平行面PAD,且BE与平面PAD所成角大于
| ||||
D、BE不平行面PAD,且BE与面PAD所成角小于
|
中心在坐标原点,焦点在x轴上的双曲线的一条渐近线方程为4x+3y=0,则该双曲线的离心率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
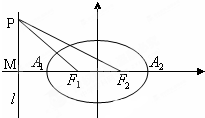 如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<
如图,已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,A1,A2为左右顶点,焦距为2,左准线l与x轴的交点为M,|MA2|:|A1F1|=6:1.若点P在直线l上运动,且离心率e<