题目内容
20．二次曲线$\left\{{\begin{array}{l}{x=3cosθ}\\{y=5sinθ}\end{array}}\right.$（θ是参数）的离心率是（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{{\sqrt{34}}}{3}$ | D． | $\frac{4}{5}$ |
分析 求出曲线的普通方程，再计算离心率．
解答 解：曲线的普通方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{25}$=1，
∴椭圆的离心率e=$\frac{\sqrt{25-9}}{5}$=$\frac{4}{5}$．
故选：D．
点评 本题考查了椭圆的参数方程，属于基础题．
练习册系列答案
相关题目
10．若P（A）=$\frac{3}{4}$，P（B|A）=$\frac{1}{2}$，则P（AB）等于（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{8}$ | C． | $\frac{1}{3}$ | D． | $\frac{5}{8}$ |
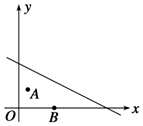如图所示，某县相邻两镇在一平面直角坐标系下的坐标为A（1，2），B（4，0），一条河所在的直线方程为l：x+2y-10=0，若在河边l上建一座供水站P，使之到A，B两镇的管道最省，那么供水站P应建在什么地方？
10．在等差数列{an}中，a3=0，a7-2a4=-1，则公差d等于（ ）
| A． | -2 | B． | $\frac{1}{2}$ | C． | 2 | D． | -$\frac{1}{2}$ |