题目内容
记等比数列{an}的前n项积为Tn（n∈N+），已知am-1am+1-2am=0，且T2m-1=512，则m= ．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由am-1am+1-2am=0，结合等比数列的性质可得am=2，从而可表示T2m-1，由此可求m的值．
解答：
解：∵am-1am+1-2am=0，∴由等比数列的性质可得，am2-2am=0
∵am≠0，∴am=2
∵T2m-1=a1a2…a2m-1=（a1a2m-1）•（a2a2m-2）…am=am2m-2am=am2m-1=22m-1=512
∴2m-1=9，∴m=5．
故答案为：5．
∵am≠0，∴am=2
∵T2m-1=a1a2…a2m-1=（a1a2m-1）•（a2a2m-2）…am=am2m-2am=am2m-1=22m-1=512
∴2m-1=9，∴m=5．
故答案为：5．
点评：本题考查了等比数列的性质，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
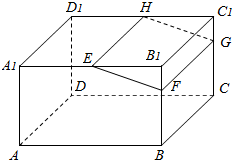如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G