题目内容
15.函数y=ax(a>0,且a≠1)在[0,1]上的最大值与最小值之和为3,则a=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 讨论0<a<1与a>1时,函数y=ax在[0,1]上的单调性,求出函数y=ax在[0,1]上的最大值与最小值,由此求出a的值.
解答 解:①当0<a<1时,
函数y=ax在[0,1]上为单调减函数,
∴函数y=ax在[0,1]上的最大值与最小值分别为1,a;
又函数y=ax在[0,1]上的最大值与最小值和为3,
∴1+a=3,解得a=2(舍去);
②当a>1时,
函数y=ax在[0,1]上为单调增函数,
∴函数y=ax在[0,1]上的最大值与最小值分别为a,1;
又函数y=ax在[0,1]上的最大值与最小值和为3,
∴1+a=3,解得a=2;
综上,a=2.
故选:A.
点评 本题考查了指数函数在闭区间上的最值应用问题,解题时要对a进行讨论,是基础题.

练习册系列答案
相关题目
5.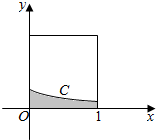 在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
附“若X~N(μ,σ2),则
P(μ-σ<X≤μ+σ)=0.6826.
p(μ-2σ<X≤μ+2σ)=0.9544.
 在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )附“若X~N(μ,σ2),则
P(μ-σ<X≤μ+σ)=0.6826.
p(μ-2σ<X≤μ+2σ)=0.9544.
| A. | 1193 | B. | 1359 | C. | 2718 | D. | 3413 |
3.将4名同学录取到3所大学,则每所大学至少录取一名的概率为( )
| A. | $\frac{4}{27}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
10.“x为无理数”是“x2为无理数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
7.设 a=${(\frac{1}{3})^{0.2}},b={2^{\frac{1}{3}}}$,则a,b 的大小关系是( )
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
4.在区间[-1,3]内任选一个实数,则x恰好在区间[1,3]内的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |